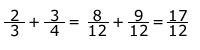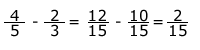| Unidad 1 | Actividad 6 |
|---|
Actividad 6. El camino más corto
Propósito
Aprenderás a realizar sumas y restas de fracciones.
¿De cuántas formas diferentes se podrá hacer una suma de fracciones?, ¿cuál de ellas será la más práctica? |
|---|
La dificultad para transitar en zonas rurales obliga a sus habitantes a buscar diferentes caminos.

| 1. | Para ir de la cabecera municipal al pueblo de Potrero Redondo hay que caminar primero |
|---|
| Inténtalo de nuevo |
|---|
| A) | Si se elige otra ruta, hay que caminar |
|---|
| B) | ¿Por cuánto es más corta? |
|---|
| Inténtalo de nuevo |
|---|
Haz clic sobre la imagen para leer el diálogo entre Abel y Andrea, que está relacionado con la forma de resolver una suma de fracciones.
|
|||
|---|---|---|---|
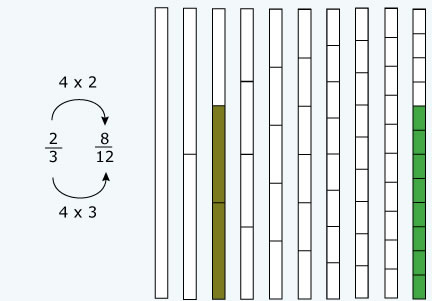
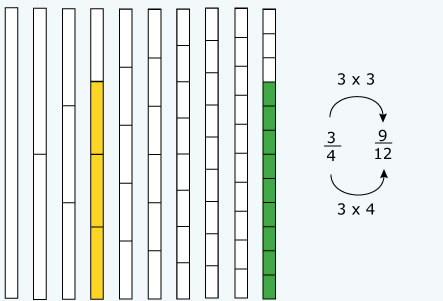
| 2. | Consulta el diagrama y señala en la tabla las fracciones que podrían hacerse equivalentes a otra al emplear el denominador que se indica en cada caso. Fíjate en el ejemplo. | |
|---|---|---|
| Fracciones | Pueden hacerse equivalentes con: |
|||||||||||
|
|
|
|
cuartos | ||||||||
|
|
|
|
sextos | ||||||||
|
|
|
|
octavos | ||||||||
|
|
|
|
décimos | ||||||||
|
¡Reflexiona tu respuesta!
¡Muy bien! |
|
|
doceavos | ||||||||
|
|
|
|
tercios | ||||||||
| 3. | Resuelve las sumas de fracciones siguientes. Primero consulta el diagrama y determina las equivalencias. |
|---|
¡Reflexiona tu respuesta! ¡Muy Bien! |
| 4. | Con base en la información del cuadro anterior, resuelve las sumas y restas siguientes. |
|---|
¡Reflexiona tu respuesta!
¡Muy Bien! |
Resolvamos otros problemas
| 5. | Zoila compró |
|---|
| Inténtalo de nuevo |
|---|
| 6. | La familia Rubio compra agua de garrafón. Cuando empezó el día el garrafón estaba lleno hasta los |
|---|
| A) | ¿Se consumió más o menos de |
|---|
| Inténtalo de nuevo |
|---|
| 7. | Resuelve las siguientes sumas y restas de fracciones. |
|---|
¡Reflexiona tu respuesta! ¡Muy Bien! |