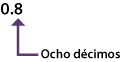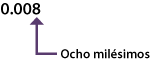Documento sin título

Unidad 2		Actividad 11

Actividad 11. En su otra presentación

Propósito

Aprenderás a representar fracciones comunes con números decimales.

		¿En tu vida cotidiana qué tanto te encuentras con las fracciones? ¿Los centímetros, los centavos y los porcentajes son fracciones?

En la vida cotidiana, constantemente recibimos información que implica el uso de datos numéricos. Es importante saber interpretar esos datos.

1.		En la tabla se muestran nueve datos que se parecen a los que frecuentemente encontramos en nuestra vida diaria.

Arrastra la etiqueta Sí a los datos que presenten medidas fraccionarias y la etiqueta No a aquellos que no las presenten.

Sí

Clavos de pulgada	Cable 75 centímetros	Paracetamol Tabletas 500 miligramos
IVA: 16%	6 metros de alambre	Tuerca de 8 milímetros
Azúcar: 0.75 de kilogramo	8 años de trabajar en la empresa	37% de preferencia electoral

Clavos de pulgada Sí	Cable 75 centímetros No	Paracetamol Tabletas 500 miligramos No
IVA: 16% Sí	6 metros de alambre No	Tuerca de 8 milímetros No
Azúcar: 0.75 de kilogramo Sí	8 años de trabajar en la empresa No	37% de preferencia electoral Sí

2.		Con tu calculadora divide el numerador entre el denominador de las fracciones de la tabla siguiente y escribe los resultados.

Haz clic en el botón Calculadora.

1	=
4

1	=
8

1	=
2

1	=
3

3	=
4

1	=
5

3	=
16

1	=
300

1	=
20

¡Reflexiona tu respuesta!

¡Muy Bien!

Las fracciones que con mayor frecuencia se encuentran en la vida diaria son fracciones decimales, que son aquellas cuyo denominador es o puede expresarse como una potencia de diez.

3.		Haz clic en el botón Calculadora y utilízala para convertir las fracciones siguientes a números decimales, escribe el resultado en el recuadro. Observa el ejemplo.

1	=	0.1
10

1	=
100

1	=
1000

3	=
10

25	=
100

72	=
1000

¡Reflexiona tu respuesta!

¡Muy Bien!

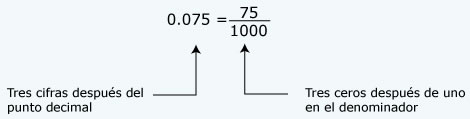
A)		Cuando se divide entre diez, ¿cuántos números se escriben a la derecha del punto decimal?

Respuesta: Una

B)		Cuando se divide entre cien, ¿cuántos números se escriben a la derecha del punto decimal?

Respuesta: Dos

C)		Cuando se divide entre mil, ¿cuántos números se escriben a la derecha del punto decimal?

Respuesta: Tres

Resolvamos otros problemas

4.		Arrastra las etiquetas a la columna correspondiente.

0.68	0.4	0.025	0.825	.893	0.3
0.75	0.003	0.04	7.5	0.068

Fracciones

Decimales

Que no son
decimales

100

1000

893

1000

Fracciones

Decimales

Que no son
decimales

0.68

100

0.75

1000

0.003

1000

0.068

1000

0.025

893

1000

.893

5.		Escribe el denominador decimal que corresponde a la fracción equivalente al número decimal que se muestra. Observa el ejemplo.

0.25	=	25
		100

0.6	=	6

0.08	=	8

0.895	=	895

0.047	=	47

0.009	=	9

0.261	=	261

0.021	=	21

0.025	=	25

0.2	=	2

0.02	=	2

0.002	=	2

0.5	=	5

0.50	=	50

0.500	=	500

¡Reflexiona tu respuesta!

¡Muy Bien!

6.		Convierte las fracciones decimales siguientes a números decimales.

6	=
10

278	=
1000

3	=
10

30	=
100

3000	=
1000

5	=
10

5	=
100

5	=
1000

¡Reflexiona tu respuesta!

¡Muy Bien!

7.		Compara la lista de productos que compraron María y Juana. Selecciona el símbolo > “mayor que” o < “menor que” o el signo = que corresponda a cada caso y colócalo en el cuadro. Fíjate en el ejemplo.

Producto	Cantidad comprada por María	Comparación	Cantidad comprada por Juana
Ejemplo: Chocolate en polvo	kilogramo	=	0.5 kilogramos
a. Jamón	kilogramo		0.6 kilogramos
b. Crema	kilogramo		kilogramos
c. Agua de jamaica	litro		0.5 litros
d. Jitomate	kilogramo		0.50 kilogramos
e. Jerga	metro		0.500 metros
f. Papas	kilogramo		0.050 kilogramos
g. Pasas	kilogramo		0.86 kilogramos

Producto	Cantidad comprada por María	Comparación	Cantidad comprada por Juana
Ejemplo: Chocolate en polvo	kilogramo	=	0.5 kilogramos
a. Jamón	kilogramo	<	0.6 kilogramos
b. Crema	kilogramo	=	kilogramos
c. Agua de jamaica	litro	=	0.5 litros
d. Jitomate	kilogramo	=	0.50 kilogramos
e. Jerga	metro	=	0.500 metros
f. Papas	kilogramo	>	0.050 kilogramos
g. Pasas	kilogramo	<	0.86 kilogramos

	A la cifra que ocupa el primer lugar después del punto decimal se le llama décimos: A la cifra que ocupa el segundo lugar después del punto decimal se le llama centésimo: A la cifra que ocupa el segundo lugar después del punto decimal se le llama milésimos: Una forma de convertir fracciones a números decimales es decir el numerador entre el denominador: Ejemplos: