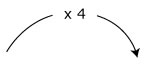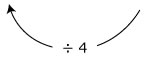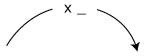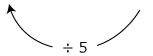Unidad 3
Actividad 16


Actividad 16. ¡Esquina, bajan!

Propósito

Identificarás situaciones de tipo proporcional.

 

¿Qué factores afectan la cantidad de gasolina que consume
un vehículo?

Las cooperativas son asociaciones de trabajo comunal que generan beneficios sociales y económicos a sus integrantes. Todos los miembros de la cooperativa son dueños de las herramientas de trabajo, y las ganancias se distribuyen equitativamente.

  

1.  

Arturo es miembro de una cooperativa que cubre varias rutas en su región. En una semana de trabajo su camioneta recorre 800 kilómetros y consume 80 litros de gasolina.

Calcula cuántos kilómetros va a recorrer y cuánta gasolina va a gastar en el transcurso de seis semanas.

  Kilómetros recorridos Litros de gasolina consumida
Semana 1
 800 80
Semana 2
 1600
Semana 3
Semana 4
Semana 5
Semana 6

Respuesta:

  Kilómetros recorridos Litros de gasolina consumida
Semana 1
 800 80
Semana 2
 1600 160
Semana 3
 2400 240
Semana 4
 3200 320
Semana 5
 4000 400
Semana 6
 4800 480


2.  

La cooperativa de transportistas inició una nueva ruta. Ahora Arturo va a recorrer 1200 km a la semana.

vg

A)   ¿Cuántos kilómetros más va a recorrer Arturo en la nueva ruta?

a)
40 km
b) 120 km
c)
400 km
d)
1200 km
  Inténtalo de nuevo  
 
 
¡Bien hecho! La respuesta es la "c"
 


B)   Si la camioneta de Arturo consume 80 l cuando recorre 800 km, ¿cuánta gasolina consume cuando recorre 1 200 kilómetros?

a)
40 l
b) 120 l
c)
400 l
d)
1200 l
  Inténtalo de nuevo  
 
 
¡Bien hecho! La respuesta es la "b"
 

vg

  En una relación entre dos cantidades, cuando una cantidad aumenta en la misma proporción que la otra, es decir, si una aumenta el doble, la otra también; o al triple, la otra también, etcétera; se dice que son cantidades que varían proporcionalmente.
   

Lee el diálogo entre Clara y Cruz sobre cómo estimar cuánta gasolina consume la camioneta de Arturo cuando recorre 1400 km.

vg

Resolvamos otros problemas


3.  

Una empresa va a regalar cuatro cuadernos por cada alumno que tenga la escuela secundaria Venustiano Carranza. Analiza la tabla siguiente y complétala.

 
Grupo Número de alumnos Número de cuadernos
1º A
 30
1º B
 25
2º A
 80
2º B
 22
3º A
 60
3º B
 10
 
 

Respuesta:

Grupo Número de alumnos Número de cuadernos
1º A
 30 120
1º B
 25 100
2º A
 20 80
2º B
 22 88
3º A
 15 60
3º B
 10 40


 

A)   ¿La relación entre el número de alumnos y el número de cuadernos es de tipo proporcional?

Sí No

B)   ¿Cuál de las opciones siguientes explica por qué?

a)
Sí, son proporcionales porque cuando la cantidad de niños aumenta al doble la cantidad de cuadernos también. Cuando tenemos diez niños y 40 cuadernos y duplicamos el número de niños, también se duplica el número de cuadernos, 20 niños, 80 cuadernos. Lo mismo pasa si
se triplica.
b)
No son proporcionales porque no aumentan de igual manera, porque cuando la cantidad de niños aumenta de diez a 22 o sea 1ños más, la cantidad de cuadernos no aumenta igual, de 40 a 88 aumentó 48.
c)
Sí, son proporcionales, porque la condición es que siempre que aumenta la cantidad de niños aumente la cantidad de cuadernos o si disminuye la cantidad dños, disminuye la cantidad de cuadernos.
d)
No son proporcionales porque cuando los alumnos se duplican, por ejemplo de diez a 20, los cuadernos también se duplican de 40 a 80, pero no lo hacen igual, los niños aumentaron en diez y los cuadernos en 40.
  Inténtalo de nuevo  
 
 
¡Bien hecho! La respuesta es la "a"
 


4.  

Una cooperativa de consumo va a repartir cinco kilogramos de maíz por cada miembro de la familia. Escribe sobre la flecha por cuál número es necesario multiplicar el número de miembros de la familia para encontrar la cantidad de kilogramos de maíz y completa la tabla siguiente:
     

Número de miembros de familia Kilogramos de maíz
2
3
4
25
6
35


Respuesta:


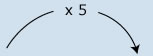
Número de miembros de familia Kilogramos de maíz
2 10
3 15
4 20
5 25
6 30
7 35



 

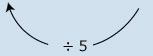
A)  

¿La relación entre el número de miembros de una familia y la cantidad de kilogramos de maíz es de tipo proporcional?

Sí No

B)   ¿Cuál de las opciones siguientes explica por qué?

a)
Sí es proporcional, porque siempre que aumenta la cantidad de miembros de la familia, aumenta la cantidad de kilogramos de tortillas. Entre más miembros más tortillas. Lo mismo sucede si disminuye la cantidad de miembros de la familia, disminuye la cantidad de tortillas.
b)
No es proporcional porque no podemos saber en la tabla si siempre que aumenta el doble o el triple el número de miembros de la familia, aumenta al doble o el triple los kilogramos de tortillas. Por ejemplo, no podemos saber si al doble de siete miembros de la familia, que serían 14, cuántos kilogramos de tortillas le corresponden.
c)
Sí son proporcionales, porque siempre que se multiplica por cinco el número de miembros de la familia, provoca que el número de kilogramos de tortillas se incremente, guardando la proporción de cinco kilogramos por cada miembro de familia. Por ejemplo, para seis miembros de la familia, corresponden 30 kilogramos de tortillas, lo cual guarda la proporción de cinco kilogramos por cada miembro,
6 x 5=30.
d)
No son proporcionales, porque al multiplicar por cinco o dividir entre cinco hace que los resultados de los miembros de la familia y la cantidad de tortillas cambie de diferente forma, por ejemplo, si la cantidad de miembros de la familia aumenta de dos a seis, aumentó en cuatro miembros y la cantidad de tortillas aumenta de 10 a 30, o sea aumentó en 20 kilos.  Las cantidades no son iguales.
  Inténtalo de nuevo  
 
 
¡Bien hecho! La respuesta es la "c"
 


5.  

Tania es una mamá que cuida mucho el desarrollo de sus hijos, por eso lleva un control del peso de su hija desde el primer año de vida hasta ño seis, que es la edad que tiene actualmente, como se muestra en la tabla siguiente.

Edad en años Peso en kilogramos
1 6
2 11
3 14
4 16
5 17
6 18


A)   ¿La relación entre la edad en años y el peso en kilogramos es de tipo proporcional? 

Sí No

B)   ¿Cuál de las opciones siguientes explica por qué?

a)
Sí es proporcional, porque siempre que aumenta la edad, también aumenta el peso.
b)
No es proporcional, porque no se puede saber cómo se incrementará en los años siguientes y ver si se cumple siempre que al duplicar o triplicar la edad, se duplica o triplica el peso.
c)
Sí es proporcional, porque cuando se duplica la edad, el peso se incrementa en la misma proporción. Por ejemplo, de uno a dos años, aumentó 5 kilos, de 2 a 4 años, aumentó 5 kilos.
d)
No es proporcional, porque el peso no aumenta siempre en la misma proporción. Al duplicar o triplicar la edad, no se duplica o triplica el peso siempre. Por ejemplo, al duplicar la edad de dos a cuatro, el peso no se duplica, de once pasa a 16, en lugar de 22.
  Inténtalo de nuevo  
 
 
¡Bien hecho! La respuesta es la "d"
 



  • Existe una relación de proporcionalidad directa entre cantidades cuando varían o cambian a partir de multiplicar ambas por el mismo número.

Ejemplo:
   
 
vg
   
  Si el cociente entre las cantidades que varían no es constante,
dichas cantidades no guardan entre sí una relación de proporcionalidad.
   
  Ejemplo:

Entre las cantidades de la tabla siguiente no existe una variación proporcional.
   
 
vg
vg