Documento sin título

Unidad 3		Actividad 19

Actividad 19. Decisiones

Propósito: Resolverás problemas de conteo y conocerás cómo se representa la probabilidad de que ocurra un evento.

		¿Cuando tomas decisiones analizas todas las posibilidades que tienes?, ¿cuando sales de viaje siempre lo haces de la misma manera?

La incertidumbre o duda que envuelve nuestra vida nos obliga a tomar decisiones; a pesar de que nunca se sabe qué es lo que va a ocurrir en el próximo instante, es mejor tomar decisiones informadas.

1.		Para ir al pueblo de Alfonso, se puede ir en camión o en tren. Si en cada una de estas opciones se puede viajar en primera o segunda clase, ¿cuántas opciones hay en total para ir al pueblo de Alfonso?

	a)	1
	b)	2
	c)	4
	d)	6

	Inténtalo de nuevo

		¡Bien hecho! La respuesta es la "c"

2.		Para hospedarse en el pueblo de Alfonso hay casas de huéspedes, posadas y hoteles; en cada una de estas opciones hay primera, segunda y tercera clase. ¿Cuántas opciones de hospedaje hay en total en el pueblo de Alfonso?

	a)	12
	b)	9
	c)	6
	d)	3

	Inténtalo de nuevo

		¡Bien hecho! La respuesta es la "b"

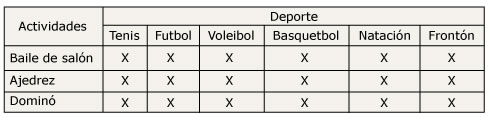
Lee la forma en que Rosa y Leticia cuentan las opciones que tienen para practicar un deporte y una actividad recreativa.

Rosa: Yo uso una tabla para organizar la información.

Club sociocultural
SALUD Y BELLEZA

Elija el deporte que más le guste y una actividad recreativa por $350.00 al mes.

• Deportes:

Tenis, futbol, voleibol, basquetbol, natación, frontón.

• Actividades recreativas:

Baile de salón, ajedrez, dominó.

Leticia: Es verdad, en ella se pueden ver todas las opciones, por ejemplo, puede ser tenis y baile de salón, tenis y ajedrez, o tenis y dominó.

Rosa: Y se pueden contar las opciones, que en total son 18.

Resolvamos otros problemas

3.		Haz clic en el botón Jugar para lanzar los dos dados y repítelo 50 veces. Observa el registro (una raya vertical I) que se coloca automáticamente en la columna de Frecuencia y en la fila que corresponda de acuerdo con la cantidad de puntos que obtendrás en cada lanzamiento, al final, cuenta las marcas en cada cantidad de puntos y escribe el resultado en la columna Total de veces.

A)		¿Cuál fue la cantidad de puntos que más salió?

Respuesta: Depende de los resultados obtenidos

B)		¿Cuál de las siguientes afirmaciones es verdadera con respecto al lanzamiento de dos dados como en la actividad anterior?

	a)	Nunca se obtendrá uno porque el mínimo número de puntos al lanzar dos dados es 2.
	b)	Siempre se obtendrá un número de puntos.
	c)	El resultado más difícil de obtener es el 12 por ser el mayor número de puntos.
	d)	Se puede obtener mayor número de puntos lanzando primero un dado y luego el otro, que si se lanzan los dos juntos.

	Inténtalo de nuevo

		¡Bien hecho! La respuesta es la "a"

4.		La siguiente tabla muestra las cantidades que se forman al combinar los dados. Analiza la información y completa la tabla.

Dado 2	Dado 1

Número de puntos	1	2	3	4	5	6
1	2	3	4	5		7
2	3	4	5		7
3	4	5		7
4	5		7
5	6	7				11
6	7				11	12

¡Bien hecho!

Respuestas:

Dado 2	Dado 1
Número de puntos	1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

A)		¿Cuál es la máxima cantidad de puntos que se forma al tirar 2 dados?

Respuesta: 12

B)		¿Existe alguna posibilidad de que caiga 13 al tirar 2 dados?

Respuesta: No

C)		¿Cuántas opciones de resultados existen al tirar dos dados?

	a)	11
	b)	12
	c)	18
	d)	36

	Inténtalo de nuevo

		¡Bien hecho! La respuesta es la "d"

D)		¿De cuántas formas puedes obtener el número 7 al tirar dos dados?

	a)	2
	b)	3
	c)	6
	d)	9

	Inténtalo de nuevo

		¡Bien hecho! La respuesta es la "c"

E)		¿De cuántas formas puedes obtener el número 7 al tirar dos dados?

Respuesta: 6 y 1; 5 y 2; 4 y 3; 3 y 4; 2 y 5; 1 y 6

F)		De las siguientes afirmaciones cuáles son correctas con respecto al lanzamiento de dos dados y los resultados que se pueden obtener.

I		El 7 es el resultado más probable porque hay 6 formas diferentes de obtenerlo.
II		El 2, 4, 6, 8, 10 y 12 son los resultados más probables porque son números pares.
III		Los resultados menos probables de obtener son 2, 3, 4, 5 y 6 porque siempre en un dado sale un número grande y en el otro un número chico.
IV		El 2 y el 12 son los resultados menos probables de obtener porque solo hay una forma de obtenerlos.
V		El 5 y el 10 tienen la misma probabilidad de obtenerse porque tienen el mismo número de formas de obtenerse.

	a)	I y III
	b)	I y IV
	c)	II y III
	d)	II y V

	Inténtalo de nuevo

		¡Bien hecho! La respuesta es la "b"

Haz clic en el botón y lee atentamente.

•	La probabilidad de que un evento ocurra puede expresarse como una fracción. Ejemplo De las 36 opciones que existen para formar cantidades al tirar 2 dados, sólo un (1) corresponde al número 12, por lo que puede decirse que existe una probabilidad de de que caiga 12.

•	Dicha cantidad puede expresarse como decimal o como porcentaje. En el ejemplo anterior, puede representarse como 0.0277 o como 2.7%.

•	La suma de la probabilidad de que suceda un evento con la probabilidad de que no suceda el mismo evento da 1 como resultado.

	En el ejemplo anterior, existe una probabilidad de de que no caiga 12, pues .

5.		Escribe en forma de fracción y número decimal la probabilidad de que al tirar 2 dados caigan las cantidades propuestas. Observa el ejemplo.

Caiga 11:		0.055

Caiga 2:
Caiga 7:

Respuesta:

Caiga 2:		0.027
Caiga 7:		0.16666

A)		Si en una apuesta tienes que elegir el número que caerá al tirar 2 dados, ¿qué número elegirías?

Respuesta: 7

•	La probabilidad es una rama de las matemáticas que estudia los fenómenos del azar.

•	A la probabilidad de que ocurra un evento o hecho se le asocia un número que va del cero al 1.



•	Por lo tanto, el número asociado a la probabilidad es cero, uno o un número fraccionario o decimal, aunque también puede expresarse como porcentaje.

•	Cuando es seguro que ocurra un evento o suceso se le asocia el número 1. Ejemplo Si trabajo es seguro que me paguen, por lo que a que me paguen le asocio el número uno.

•	Cuando es seguro que NO ocurra un evento o suceso se le asocia el número cero. Ejemplo Si tiro dos dados es seguro que no caiga el número uno, pues la mínima cantidad que se puede formar con los puntos de dos dados es dos.