| |
| Unidad 4 |
 |
Actividad 21 |
Actividad 21. Lo superficial
Propósito.
Calcularás el área de superficies rectangulares.
 |
|
¿Alguna vez has calculado el área de una pared o superficie?
¿En qué oficios se utiliza la medición de superficies? |
Una parte importante del trabajo de albañilería es calcular el área de las superficies y determinar cuánto material se requiere. Por ejemplo, determinar cuántos mosaicos se necesitan para cubrir
una superficie. |
|
 |
| 1. |
|
Clemente coloca mosaico en baños. Ayuda a Clemente a saber cuántos mosaicos cubren cada superficie. En cada caso arrastra los mosaicos
a la superficie para cubrirla, contesta las preguntas y haz clic en el botón Superficie para que compares las superficies. |
| G) |
|
¿Cuántos mosaicos necesita Clemente para cubrir la superficie 5? |
| H) |
|
¿Cuántos centímetros mide por lado un mosaico? |
Haz clic en el botón y analiza lo que hace Clemente para saber cuántos mosaicos va a ocupar para la superficie 6.
• Para medir el área de cuadrados y rectángulos, se utilizan unidades cuadradas.
• El metro cuadrado es una de las unidades que más se utilizan para medir superficies. El metro cuadrado es el área de un cuadrado que mide un metro de cada lado.
• La abreviatura del metro cuadrado es: m2.

Resolvamos otros problemas
| 2. |
|
Adalberto y Ramón son pintores de casas y edificios. Para hacer los presupuestos que les solicitan, tienen que determinar el tamaño del área que van a pintar en metros cuadrados. |
Haz clic en los botones para que veas las dimensiones de cada pared y calcules
su área.
Completa la tabla siguiente; escribe las dimensiones y el área de cada pared. Observa el ejemplo.
Respuesta:
| |
Base |
Altura |
Área |
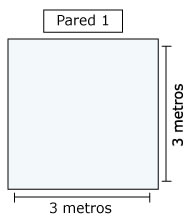
| Pared 1 |
3 m |
3 m |
9 m2 |
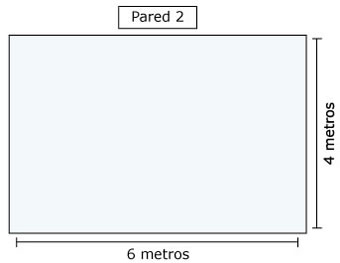
| Pared 2 |
6
m |
4
m |
24
m |
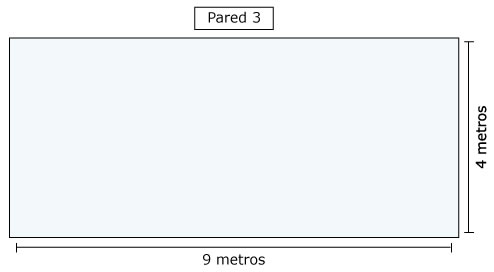
| Pared 3 |
9
m |
4
m |
36
m |
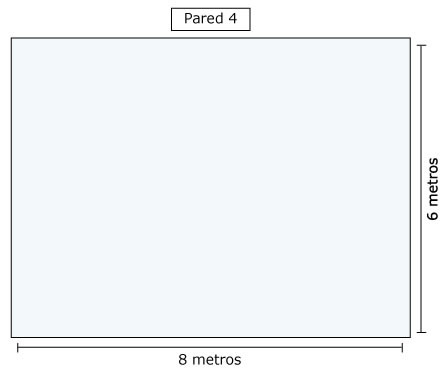
| Pared 4 |
8
m |
6
m |
48
m |
| A) |
|
Con base en la información de la tabla, ¿cuáles de las afirmaciones siguientes son verdaderas? |
| I |
|
El área de la pared 2 es el triple de la pared 1. |
| II |
|
El área de la pared 1 es la cuarta parte de la pared 3. |
| III |
|
El área de la pared 4 es el doble de la pared 2. |
| IV |
|
El área de la pared 3 es 25% más pequeña que la pared 4. |
| V |
|
El área de la pared 1 es 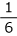 de la pared 4. |
| |
 |
|
¡Bien hecho! La respuesta es la "c" |
|
|
| B) |
|
Ellos cobran a $45.00 el metro cuadrado, ¿cuánto recibirán por pintar todas las paredes? |
| |
 |
|
¡Bien hecho! La respuesta es la "d" |
|
|
| 3. |
|
Águeda va a vender dos tapetes decorativos. Uno es cuadrado y mide 70 cm por lado; el otro es rectangular y mide 65.5 cm de un lado y 56.5 cm
del otro. |
Haz clic en el botón Calculadora si necesitas utilizarla.
| A) |
|
¿Qué unidad de medida usarías para medir la superficie de los tapetes? |
| |
 |
|
¡Bien hecho! La respuesta es la "d" |
|
|
| B) |
|
¿Cuál es el área del tapete cuadrado? |
| |
 |
|
¡Bien hecho! La respuesta es la "c" |
|
|
| C) |
|
¿Cuál es el área del tapete rectangular? |
| |
 |
|
¡Bien hecho! La respuesta es la "d" |
|
|
| D) |
|
El precio por cada centímetro cuadrado (cm2) de los tapetes es de $0.50, ¿cuál es el precio del tapete cuadrado? |
| |
 |
|
¡Bien hecho! La respuesta es la "c" |
|
|
| E) |
|
¿Cuánto cuesta el tapete rectangular? |
| |
 |
|
¡Bien hecho! La respuesta es la "d" |
|
|
| 4. |
|
Un cliente le encargó a Águeda un tapete que tuviera una superficie de
4000 cm2 y que uno de sus lados midiera 80 cm, ¿cuál será la medida del otro lado del tapete? |
| |
 |
|
¡Bien hecho! La respuesta es la "b" |
|
|
 |
| |
Para calcular el área de un rectángulo se multiplica la longitud de su base por la longitud de su altura. |
|
| |
|
|
| |
Área= base x altura
|
|
| |
|
|
| |
La fórmula se puede abreviar de la manera siguiente : |
|
| |
|
|
| |
A = b x h
|
|
| |
|
|
| |
Por ejemplo, para conocer el área de un rectángulo que tiene 6.8 cm de base y 4.9 cm de altura se multiplica: |
|
| |
|
|
| |
6.8 cm x 4.9 cm = 33.32 cm2
|
|
| |
|
|
| |
El área de dicho rectángulo es de 33.32 cm2.
Para calcular el área de un cuadrado se hace de la misma forma que con el rectángulo, pero como sus dos lados miden lo mismo, entonces la fórmula es: |
|
| |
|
|
| |
Área = lado x lado |
|
| |
|
|
| |
En forma abreviada: |
|
| |
|
|
| |
A = L x L
A = L2
|
|
| |
|
|
| |
Donde L2 significa multiplicar la medida del lado por sí misma. |
|
|
 |
|
|