| En un sistema de ejes cartesianos, cada punto se describe
mediante sus coordenadas.
Mueve el punto A
para que sus coordenadas sean A(-2,1). |
|
|
|
Dados los puntos A y B, la flecha que va de A a B se llama
vector, se representa por
 .
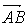A es el
origen del vector y B el extremo.
Para calcular las coordenadas del vector AB, se restan las
coordenadas del extremo menos las del origen.
Si el origen del vector es el origen de
coordenadas (0,0), las coordenadas del extremo son las
coordenadas del vector. |
CARACTERÍSTICAS DE UN VECTOR.
|
Módulo,
es la longitud, se representa por
|AB|
Dirección,
es la de la recta que lo contiene.
Sentido,
el que va del origen al extremo.
Puedes modificar el Modulo, dirección (desde
la recta) y sentido del vector AB. |
|
La dirección y sentido de un vector se expresan numéricamente
mediante el argumento, ángulo que
forma el vector con el semieje positivo del eje de abscisas OX.
| Cálculo del módulo y argumento de
un vector. Sea V(x,y) el vector, del que se conocen
sus coordenadas x e y.
Modulo;
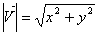
Argumento;
 |
|
|
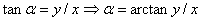Ejercicio.
Determina el módulo de los vectores a) (1,1) b) (-1,1) c) (0,2)
Escribe las coordenadas de dos vectores diferentes de módulo 5.
|
|
|
