|
Los triángulos de la figura tienen un ángulo común A,
los lados opuestos a A son paralelos.
Los triángulos encajados como éstos se dice que están en posición de
Tales.
Mueve el botón para ver que estamos en las condiciones
que enuncia el teorema de Tales. Se tiene por tanto:
|
|
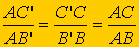
Dos triángulos son semejantes si tienen los mismos ángulos y los lados
correspondientes proporcionales.
DOS TRIÁNGULO EN POSICIÓN DE TALES SON
SEMEJANTES.
|
Sus ángulos son iguales.
A es ángulo común. B=B' y C=C' por
ser ángulos correspondientes entre rectas paralelas.
|
Aplicando el teorema de
Tales |
|
| |
|
|
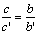
Si desplazamos el
triángulo a'b'c' (mueve el punto verde) |
 |
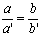De
estas dos expresiones se tiene:
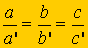
Esto es, sus lados son proporcionales.
|
|
CRITERIOS DE SEMEJANZA DE TRIÁNGULOS. Para que dos triángulos sean
semejantes es suficiente con que se verifique una de las siguientes
condiciones:
|
1.-Dos triángulos son semejantes si
tienen dos ángulos iguales.
|
2.-Dos triángulos son semejantes si
tienen dos lados proporcionales e igual el ángulo que forman. |
3.- Dos triángulos son semejante si
sus
lados son proporcionales. |
|
 |
 |
|
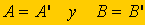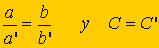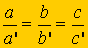Demostración gráfica del criterio 1. De forma similar pueden
demostrarse los otros dos.
Puedes mover los puntos
 . Parar y reanudar la
construcción desde los controladores de la parte inferior o situando el
cursor dentro/fuera del cuadro.
|
|
|
