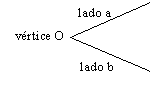
ÁNGULOS
DEFINICIONES:
Ángulo: del Latín 'angulus', rincón.
Intuitivamente, desde un punto de vista estático, la idea de ángulo traduce la mayor o menor abertura de dos semirrectas a y b, llamadas lados, que parten de un mismo punto O, llamado vértice.
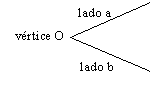
Dos ángulos son iguales si al superponer sus vértices coinciden sus lados respectivos (sin importar el orden).
Se puede establecer una correspondencia biyectiva entre los ángulos de un plano y los sectores, o con los arcos, de una circunferencia de radio unidad:
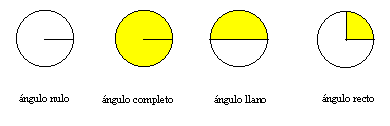
Ciertos ángulos, como los de la figura adjunta, reciben nombres especiales:
Para medir un ángulo se utiliza el arco que determinan los lados en la circunferencia cuyo centro es el vértice.
Si la unidad de medida del arco es el radio de la circunferencia, se dice que el ángulo se mide en radianes; así que un ángulo completo mide 2p radianes, ya que la longitud de la circunferencia es 2p r, siendo r su radio.
Si la circunferencia se divide en 360 partes iguales, cada parte se denomina un grado sexagesimal.
Si la circunferencia se divide en 400 partes iguales, cada una se llama un grado centesimal.
Los ángulos menores que un recto, se llaman agudos y los mayores que un recto se denominan obtusos.
Algunos ejemplos de medidas de ángulos:

Para sumar dos ángulos, se superponen sus vértices y el segundo ángulo se coloca a continuación del primero, de modo que tengan un lado común. Si la suma pasa de un ángulo completo, entonces se elimina este y nos quedamos sólo con la parte restante.
Los ángulos tal como acabamos de definirlos (que suelen llamarse sectores ángulares) pueden caracterizarse por un par de semirrectas, sin importar el orden.
Si se considera, dinámicamente, que un ángulo representa una rotación, entonces los ángulos tienen signo, según se considere que la semirrecta a gira hacia la semirrecta b, o al contrario:
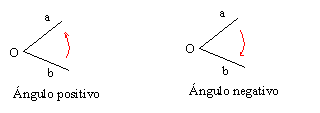
Estos ángulos orientados se pueden representar por un par ordenado de semirrectas: a^b. El ángulo a^a representa el ángulo nulo.
Ahora, para sumar dos ángulos hay que colocar la primera semirrecta del segundo ángulo sobre la segunda del primero). Se cumple la relación de Chasles:
a^b + b^c =a^c
y, por tanto:
a^b=-b^a
COMENTARIOS:
La Naturaleza y el Arte parecen preferir ángulos de 72º, 120º, 90º y 60º. El primero suelen preferirlo muchas flores; el segundo es muchas veces el resultado del cuarteamiento de superficies, …
Nota: Además de las fotos que aquí se presentan, pueden analizarse las del apartado de polígonos
RELACIONES:
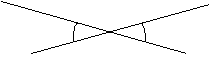
Ángulos opuestos por el vértice:
Dos rectas que se cortan, determinan ángulos iguales.
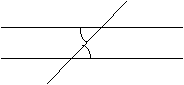
Ángulos alternos internos:
Dos rectas paralelas cortadas por otra recta determinan ángulos iguales,
Ángulos en un polígono:
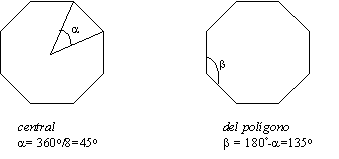
Ángulos en una circunferencia:
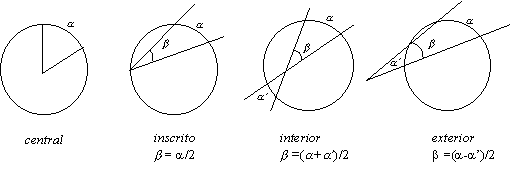
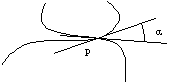
Ángulo entre dos curvas que se cortan:
Es el ángulo que forman las rectas tangentes, si existen, a las curvas en el punto de corte P
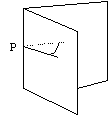
Ángulo diedro entre dos planos que se cortan:
Es el ángulo que forman una semirrecta contenida en uno de los planos, perpendicular a la recta intersección por un punto P, y otra semirrecta, contenida en el otro plano, perpendicular a la recta intersección por el mismo punto P.
Por ejemplo, el angulo diedro que forman entre si cada dos caras consecutivas de un cubo es 90º; el ángulo diedro de las caras de un tetraedro es
Ángulo de una recta y un plano:
Es el ángulo que forma la recta con la recta intersección del plano que pasa por aquella y es perpendicular al plano.
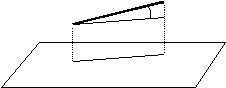
Ángulo de dos superficies en un punto de intersección:
Es el ángulo que forman sus planos tangentes en el punto de intersección, si existen.
Ángulo sólido:
Es el espacio comprendido dentro de una superficie cónica (o piramidal).
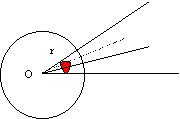
Para medir un ángulo sólido, se traza una esfera de radio r y centro el vértice O del ángulo. Si S es el área de la superficie esférica interceptada por el ángulo sólido sobre la esfera, el cociente S/r2 es el valor del ángulo sólido en estereorradianes. Como la superficie de la esfera es 4p r2, la medida de un ángulo sólido completo es 4p estereorradianes.