SIMETRÍA

DEFINICIONES:

Al observar muchas de las formas de nuestro mundo es frecuente descubrir que pueden considerarse generadas por la repetición de una sus partes, colocadas en distintas posiciones, siguiendo unas pautas. Decimos entonces que la forma es simétrica.

En cada una de estas figuras, se puede imaginar movimientos que, al aplicárselos, las dejan invariantes, es decir, tal como están, aunque permuten sus partes.

Se precisa algo más estas ideas:

Transformación geométrica

Es una correspondencia (una regla) que asocia a cada punto del plano (o del espacio) un punto y sólo uno del plano (o del espacio), de modo que si al punto A le corresponde el B, entonces al B le corresponde A.

Si un punto se transforma en sí mismo, se dice que es invariante o doble.

El resultado de aplicar una transformación T, seguida de otra S es la transformación compuesta SoT (también llamada producto de T y S).

Movimientos

Una transformación geométrica que conserve las distancias entre los puntos es un movimiento. También se llama isometría y congruencia.

Una rotación en el plano, de centro O y ángulo 90^º es un movimiento que transforma la L vertical en la misma L tumbada, tal como se indica en la figura adjunta:

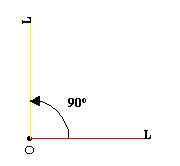
Fig 10_2

El punto O es invariante en la rotación anterior. El ángulo puede ser cualquiera.

Una traslación de vector es un movimiento que transforma la L en la L desplazada paralelamente según el vector dado:

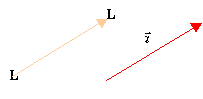
Fig 10_3

En una traslación no hay ningún punto invariante.

Una reflexión es una isometría que deja invariante todos los puntos de una recta que se denomina eje de simetría o espejo. La figura L se transforma en su imagen en el espejo:

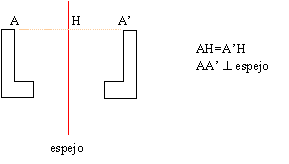
Fig 10_4

Una reflexión con deslizamiento es el producto de una reflexión en el espejo r y de una traslación a lo largo de la recta r:

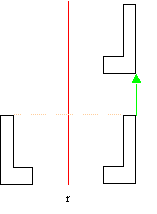
Fig. 10_5

De manera análoga, pueden definirse movimientos en el espacio:

Una rotación de eje r y ángulo a es una isometría que transforma cada punto A del espacio en otro A’, tal que en el plano que pasa por A, A’ y es perpendicular al eje de rotación r, A’ es la imagen de A por la rotación plana de centro la intersección del eje y del plano y ángulo

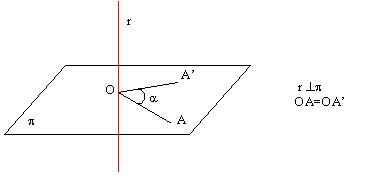
Fig 10_6

Una reflexión en el espacio es una isometría que deja invariante todos los puntos de un plano que se denomina plano de simetría o espejo. La figura L se transforma en su imagen en el espejo:

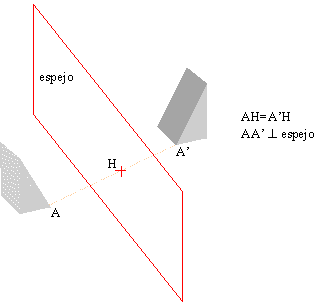
Fig 10_7

Una traslación en el espacio se define de igual manera que en el plano.

Existe una transformación especial, la transformación identidad, es decir aquella que transforma cada punto en sí mismo, que es un movimiento, ya que conserva las distancias entre puntos

Formas simétricas

Una forma es simétrica si es posible reproducirla a partir de una de sus partes mediante movimientos sucesivos. O lo que es lo mismo: una forma es simétrica si le podemos aplicar movimientos que la dejan invariante.

Por ejemplo:

La letra A tiene un eje de simetría vertical. La letra E tiene un eje de simetría horizontal. Ambas tienen simetría bilateral:

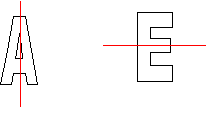
Fig. 10_8

Las letras O, X, H tienen dos ejes de simetría que se cortan y, por tanto, un centro de simetría:

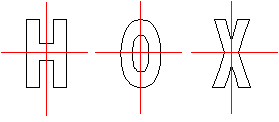
Fig 10_9

En cambio, las letras N y Z sólo son simétricas por una rotación de 180^º , con centro en el punto medio:

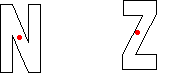
Fig 10_10

Pero no tiene simetría bilateral.

Obsérvese que en las figuras con simetría bilateral es posible colocar un espejo plano de modo que se puede superponer la imagen y la forma original:

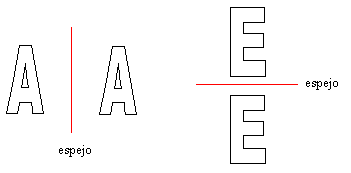
Fig.10_11

En cambio, esto no es posible en las que no poseen dicho tipo de simetría:

Fig. 10_12

Esto nos permite dar una nueva caracterización de las figuras con simetría bilateral: Una forma tiene simetría bilateral si puede superponerse punto a punto a sus imágenes en un espejo plano.

El grado de simetría de una forma se mide pon el número de movimientos que la dejan invariante. El número de planos de simetría, en el caso espacial; y el número de ejes de simetría, en el caso plano, será un índice de dicho grado.

Otras transformaciones geométricas:

Además de los movimientos, que conservan las distancias entre los puntos, se definen otros tipos de transformaciones que no conservan las distancias. Así:

Una homotecia de centro O y razón k asocia a cada punto A del plano (o del espacio) el punto A’ tal que . La razón k es un número real positivo o negativo.

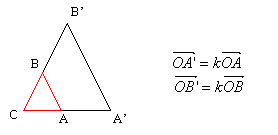
Fig. 10_13

Una semejanza de razón k, k>0, es una transformación geométrica tal que si a le corresponde A’ y a B le corresponde B’, entonces la distancia de A’ a B’ es k veces la distancia de A a B:

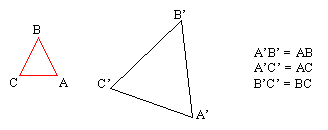
Fig. 10_14

Tanto en una homotecia como en una semejanza, se conserva el valor de los ángulos (no orientado) que se corresponden.

Pueden definirse transformaciones que no conserven ni la distancia ni los ángulos.

En las fotografías que aquí se presentan puede observarse diversos tipos de transformaciones geométricas.

COMENTARIOS:

Simetría bilateral

La simetría bilateral es la simetría que todo el mundo conoce como simetría sin más. La simetría bilateral sucede cuando dos partes de un todo son imagen especular una de la otra. Por ello esta simetría también es conocida como simetría especular. Por ejemplo, el ala izquierda de una mariposa, reflejada en un espejo, reproduce la mariposa completa. Lo mismo ocurre con su ala derecha, decimos entonces que la mariposa es simétrica. Otros ejemplos de simetría especular podemos encontrarlos en los animales superiores (como el tigre, león, caballo, ser humano), en las hojas de la mayoría de las plantas, o los reflejos en las aguas calmadas de un lago.

Movimiento y forma

La necesidad de avanzar en una dirección ha causado un desarrollo diferenciado entre la parte delantera y la espalda de animales superiores (mamíferos, aves, peces, reptiles y anfibios) e insectos, al tiempo que exige que la derecha y la izquierda sean iguales. Si no existiera simetría el movimiento sería helicoidal y no existiría la simetría bilateral.

Los artefactos humanos dotados de movimiento direccional, también necesitan este tipo de configuración, que se altera sólo mínimamente en algunos detalles. Por ejemplo un coche con un solo espejo retrovisor externo en un lateral, un barco, un avión, etc.

Los objetos que diseñados para moverse en dirección vertical pueden tener diferentes su parte superior e inferior, pero deben tener simetría cilíndrica, es decir todo es igual alrededor del eje vertical. Por ejemplo un globo aerostático, la umbela de una medusa,... Lo mismo ocurre a los troncos de los árboles aunque la dirección vertical es marcada por la gravedad, no por el movimiento.

La simetría de traslación se observa especialmente en los vegetales en los que los brotes y las hojas se repiten de manera periódica con el crecimiento. También en los cienpiés y alguno insectos.

La simetría cilíndrica se da en ausencia de gravedad, y cuando es necesario el movimiento direccional, se diferencian la parte anterior y posterior pero se da simetría cilíndrica de eje horizontal: algunos peces, zepelín,...

La simetría esférica es característica de los seres vivos más pequeños o de pequeñas cantidades de fluidos flotando en el seno de otro. Cuando hay simetría esférica todo es igual en todas direcciones. Ejemplo: granos de polen

La simetría radial es propia de seres en los que influye también una sola dirección. Por ejemplo la mayoría de las flores, las copas de los árboles, por ausencia del movimiento direccional; los erizos, ofiuras, estrellas, anémonas, medusas, todos ellos animales marinos que no sufren el efecto de la gravedad, pero sufren la presión hidrostática y tampoco tienen definido un sentido de marcha.

Análogamente a lo que ocurre con el movimiento si no hay simetría, sucede en el crecimiento (petrificado movimiento según Octavio Paz), por ello las caracolas tienen forma concoespiral.

De manera general, parece que todas las simetrías de los seres vivos suponen una economía en el mensaje genético.

Formas enantimorfas

Si un objeto gira en un sentido, su imagen en un espejo gira en sentido contrario:

Fig10_15

En la naturaleza hay formas que existen por parejas, la forma y su imagen. Por ejemplo: las dos manos, tijeras para diestros y zurdos, los pares de zapatos, … Estas parejas de formas, simétricas una de otra, se llaman enantimorfas.

RELACIONES

Producto de reflexiones

Hemos visto anteriormente que el producto, o composición, de transformaciones consiste en la aplicación sucesiva de las transformaciones dadas. Vamos a efectuar el producto de dos reflexiones, S₁ y S₂, en los dos casos posibles:

Los espejos de ambas son paralelos.

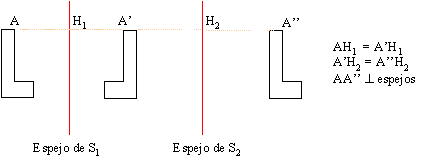
Fig. 10_16

Así que, el producto de S₁ por S₂ es una traslación de vector

Reciprocamente: toda traslación la podemos considerar como el producto de dos reflexiones paralelas.

Los espejos de ambas se cortan:

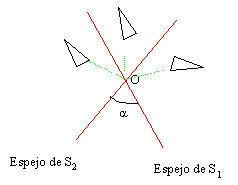
Fig. 10_17

Aquí, el producto de ambas reflexiones es una rotación de centro O (punto de intersección de los espejos) y ángulo igual al doble del que forman ambos espejos.

Recíprocamente: toda rotación puede considerarse como el producto de dos reflexiones.

Grupos de simetrías

El conjunto de todos los movimientos del plano (o del espacio), con la operación producto anteriormente definida, posee las siguientes propiedades:

El producto de dos movimientos es otro movimiento.

Dados tres movimientos A, B y C, se verifica la propiedad asociativa: (AoB)oC = Ao(BoC).

El movimiento identidad, I, verifica: AoI=IoA, para cualquier movimiento A.

Para todo movimiento A existe otro, A^-1, llamado su inverso, tal que: AoA^-1 = A^-1oA = I

Estas cuatro propiedades se resumen diciendo que el conjunto de los movimientos, con el producto, es un grupo.

No es difícil demostrar que el conjunto de movimientos que dejan invariante una forma dada siempre es un grupo, que se llama grupo de las simetrías de la forma.

De esta manera, puede demostrarse que:

Hay 7 maneras distintas esencialmente de repetir un diseño en una cinta. O lo que es lo mismo, hay 7 grupos de simetría unidimensionales.

Hay 17 grupos de simetría para los mosaicos, esencialmente distintos, en el plano bidimensional.

Hay 32 grupos de simetría para las retículas espaciales de los cristales, esencialmente distintos, en el espacio tridimensional.