CIRCUNFERENCIA Y CÍRCULO

DEFINICIONES:

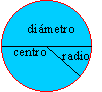
La circunferencia es una figura plana cuyos puntos están a una misma distancia de un punto llamado centro. La circunferencia y los puntos de su interior forman el círculo. Por tanto, los puntos del círculo distan del centro un radio o menos.

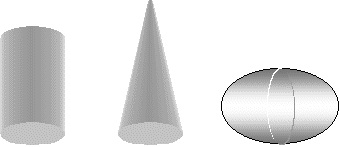
Tiene infinitos ejes de simetría que pasan por el centro: son los diámetros. Circunferencias y círculos pueden obtenerse como secciones de la esfera, de un cilindro, de un cono, de un elipsoide, …

De una manera dinámica, pueden generarse como la estela que deja un segmento al girar si uno de los extremos se mantiene fijo.

En las figuras adjuntas pueden observarse algunos elementos de la circunferencia y del círculo:

COMENTARIOS:

El horizonte en altamar es un círculo cuyo centro es la persona que lo observa.

La mayoría de las formas vivas están relacionadas con el círculo. Si las condiciones de crecimiento fueran las mismas en todas las direcciones de cada plano (isotropía), las secciones de los cuerpos serían círculos perfectos.

Una piedra lanzada en un estanque de agua, una perturbación sonora o electromagnética, en un punto del espacio, provoca ondas que se propagan formando frentes de ondas circulares.

La rueda es la base del movimiento.

La circunferencia y la esfera han inspirado no pocas ideas acerca de la infinitud. Así, el cardenal alemán Nicolás de Cusa (1401-1464) describía el universo como "una esfera cuyo centro se encuentra en todas partes y la circunferencia en ninguna."

RELACIONES:

Posiciones relativas de una recta y una circunferencia:

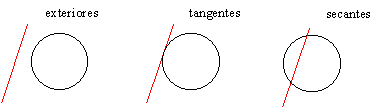
Posiciones relativas de dos circunferencias:

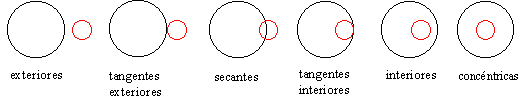
Circunferencias que pasan por un punto y por dos puntos dados del plano:

Por un punto, P, pasan infinitas circunferencias. Por dos puntos, P y Q, pasan infinitas circinunferencias cuyos centros están en la mediatriz del segmento que une aquellos puntos.

Centro de una circunferencia:

Dada una circunferencia cuyo centro desconocemos, podemos hallarlo así: (1) Escojamos tres puntos de ella, A, B y C. (2) Tracemos las mediatrices (perpendiculares por el punto medio) de los segmentos AB y BC. El punto de corte, O, de ambas, es el centro buscado

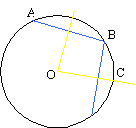
Tambien puede determinarse mediante el corte de dos diámetros ayudandonos para ello de un espejo, o doblando el papel en el que está dibujada.

Círculos tangentes a un círculo del mismo radio:

Si la disposición es como la que sigue, hay 4 círculos tangentes a uno dado:

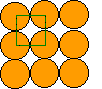
En esta otra disposición, cada círculo tiene a su alrededor 6 círculos tangentes:

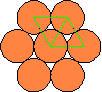
Longitud de la circunferencia de radio r: 2p r

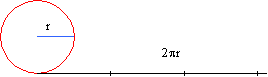
Área del círculo de radio r: p r².

Podemos imaginar que el círculo es como una rodaja de cebolla, formada por circunferencias concéntricas. Al efectuar un corte transversal que pase por el centro, y rectificar las infinitas circunferencias, obtendremos un triángulo cuya base es 2p r y cuya altura es r, de modo que el área será (2p r.r)/2= p r².

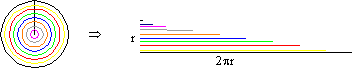
Arco capaz:

Dado un ángulo a y dos puntos A y B, se llama arco capaz relativo al ángulo y los puntos, al conjunto de puntos del plano desde los que se ve el segmento AB bajo un ángulo a . La construcción de un arco capaz es la que sigue:

Se puede expresar la circunferencia como el lugar geométrico de pares de números reales que cumplen una ecuación.