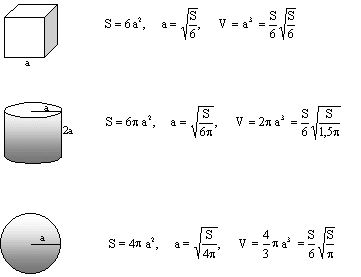
DEFINICIONES:
La esfera es una superficie cuyos puntos están a la misma distancia, llamada radio, de un punto llamado centro de la esfera. El conjunto de todos los puntos de la esfera y de los puntos que encierra en su interior es una bola. Por tanto, los puntos de una bola distan del centro un radio o menos.

Hay infinitos planos que cortan a la esfera según circunferencias. Si pasan por su centro son circunferencias máximas, cuyos diámetros son los ejes de simetría de la esfera; se llaman diámetros de la esfera Todos los diámetros pasan por el centro de la esfera.
Una esfera puede generarse al hacer girar una circunferencia alrededor de uno de sus diámetros.
A veces, sólo observamos una parte de la esfera: casquetes, zonas, sectores, lunas, triángulos o de una bola: segmentos y anillos esféricos .
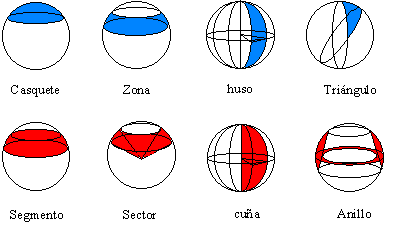
COMENTARIOS:
La forma esférica la adoptan muchos organismos unicelulares, los huevos de los animales, los frutos, las pompas de jabón, las gotas de lluvia, los planetas..., con más o menos aproximación. La forma esférica cumple una función general en multitud de instrumentos: como los rodamientos en las máquinas; boyas, etc.
La forma esférica revela la homogeneidad y simetría en todas las direcciones de las fuerzas que la producen y economiza el mensaje genético. Otras veces representa una ventaja en el proceso de la selección natural: la forma de los huevos de todos los animales permite minimizar las perdidas de calor (para una superficie dada, máximo volumen) y es difícil de morder por los depredadores.
RELACIONES:
Cortes planos de la esfera:
Siempre se obtienen circunferencias. Si el corte pasa por el centro de la esfera, entonces las circunferencias son de radio máximo (igual al de la esfera).

Sombras de una esfera:
Según la forma de iluminar las esferas, se obtienen sobre una plano circunferencias o elipses.
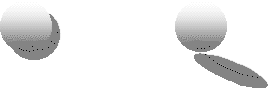
Apilamiento de esfera iguales:
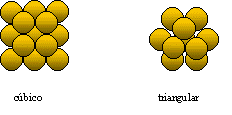
Cada bola está rodeada de 12 bolas tangentes a ella. En el caso cúbico, queda más espacio vacío entre las bolas que el caso triangular. Este último es pues más compacto que el primero. En el caso triangular, los centros de cada cuatro bolas tangentes forman un tetraedro y, como los tetraedros no macizan el espacio sino que dejan huecos, se podrían obtener apilamientos más compactos. La optimización del apilamiento de esferas es hoy un problema sin resolver.
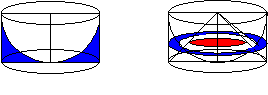
Volumen de la bola de radio r:
4/3(pi)r3
En efecto, en las dos figuras que siguen, puede observarse que, al ser iguales las secciones de la escudilla y de la semiesfera, y teniendo en cuanta que el volumen de un cono es un tercio del área de la base por la altura, se obtiene la relación anterior.
Área de la esfera de radio r:
4(pi)r2
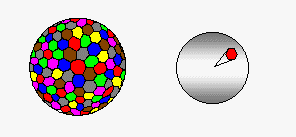
Para intuir esta relación, podemos imaginar la bola de radio r descompuesta en conos pirámides) de bases B1, B2, …, Bn y altura r. El volumen total de todos los conos es:
y, para n tendiendo a infinito, la suma de todas las bases es la superficie de la esfera, S, y el volumen de los infinitos conos es el de la bola. Así que:
![]()
y, de aquí, se obtiene S=4(pi)r2.
Superficie mínima:
Para una misma superficie S, la esfera tiene un volumen máximo, respecto a otros cuerpos. Por ejemplo, si V es el volumen, se obtiene: