DEFINICIONES:
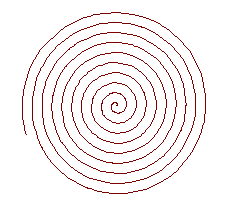
Una espiral es una curva plana y abierta que da indefinidamente vueltas alrededor de un punto (origen de la espiral), alejándose de él, o aproximándose.
Algunas veces puede leerse esta versión: una espiral es una curva que comienza en un punto origen y cuya curvatura disminuye, o aumenta, constantemente. Pero esta definición dejaría fuera las espirales poligonales.
De manera general, la punto forma un hélice es una curva espacial alabeada cuya dirección (la de la tangente) en cada ángulo constante con una dirección fija.
La hélice cilíndrica es una hélice arrollada sobre un cilindro de revolución. Corta a todas las generatrices del cilindro formando ángulos iguales.
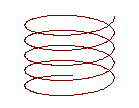
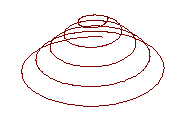
La hélice cónica es una hélice sobre un cono de revolución.
COMENTARIOS:
La espiral se expande en un plano, ocupando el mayor espacio posible. La espiral es enormemente versátil, se observa en las galaxias y en los virus; son espirales orgánicas los cuernos de los rumiantes y los caracoles , las conchas de los moluscos (por ejemplo: el Nautilus); nummulites fósiles, puede observarse en el girasol, piñas, contorno de algunas hojas cordiformes, trompas y colas en reposo, rollos, serpientes, turbulencias de los huracanes, desagües de las bañeras, tirabuzones, ...
Las hélices sirven de anclaje: zarcillos (por ejemplo del dondiego de día, de la madreselva, del lúpulo, de la vid), cocoteros, fibras, cabellos, tornillos, cuerdas, braceas de las piñas, ‘espirales’ de los cuadernos, muelles y sacacorchos , cuernos, colas y trompas en uso de muchos animales, la barandilla de una escalera de caracol, la trayectoria del Sol en el espacio, el ADN, …
Tanto las espirales como las hélices, pueden girar hacia la izquierda o hacia la derecha, lo que da lugar a espirales y hélices dextrogiras y levogiras.
RELACIONES:
Espiral de Arquímedes o aritmética:
El radio vector r es proporcional al ángulo de giro q: r = aq
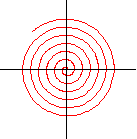
Puede considerarse generada por un punto que, partiendo del origen O (polo)se aleja del origen con una velocidad constante y, al mismo tiempo, gira con una velocidad angular constante. El coeficiente a es el cociente de la primera por la segunda velocidad.
Son espirales de Arquímedes, la de nuestra galaxia, las trompas y colas de algunos seres vivos, en reposo, los nummulites, adornos de muchos dibujos y esculturas.
Espiral equiangular o logarítmica o geométrica:
El radio vector depende exponencialmente del ángulo de giro:
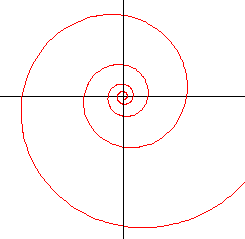
Mientras los ángulos crecen en progresión aritmética, los radios lo hacen en progresión geométrica.
Ejemplos de este tipo de espiral son: la concha del Nautilus, algunos dibujos y esculturas, el testero de un violín, trayectoria descrita por algunos insectos atraídos por un punto luminoso, …
Espiral hiperbólica o reciproca:
El radio vector depende inversamente del ángulo de giro: rq = a
Puede observarse que la espiral crece pero nunca pasa de la asíntota y=a.
Espiral áurea rectangular o de Durero:
Construyamos un rectángulo áureo AFGD, a partir del cuadrado ABCD, tal como se indica en la figura adjunta (E es el punto medio del segmento DC).
Si AD = 1, entonces EG=EB=
Por tanto:
DG=DE+EG=
. Éste es
el número áureo f El rectángulo áureo AFGD tiene la notable
propiedad de que el rectángulo BFGC también es áureo, ya que
la proporción entre su lado mayor y menor es el número áureo.
De la misma manera, con este rectángulo podemos obtener un nuevo
rectángulo áureo a menor escala. Y así, sucesivamente.
Trazando arcos de circunferencia en cada uno de los cuadrados de
los rectángulos áureos, se obtiene la espiral rectangular
áurea. o de Durero:
Se genera por un punto que gira alrededor de un eje en el espacio y, a la vez, se desplaza paralelamente al mismo. Hay pues un giro y una traslación simultáneos.
Respecto a un sistema de referencia cartesiano ortonormado en el que el eje z coincide con el del cilindro de la hélice, las ecuaciones son (ver figura anterior):
siendo |h| el paso de la hélice (distancia que separa dos puntos consecutivos de la hélice sobre una misma generatriz del cilindro.
Se genera por un punto que gira alrededor de un eje en el espacio y, a la vez, se desplaza sobre el cono paralelamente al mism. Hay pues un giro y una traslación con contracción simultáneos.
Respecto a un sistema de referencia cartesiano ortonormado en el que el eje z coincide con el del cóno de la hélice, las ecuaciones son (ver figura anterior):
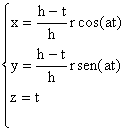
Espirales poligonales:
Pueden construirse espirales como las de la figura, a partir de triángulos, pentágonos, etc.
Espiral multipoligonal
