PARALELISMO
DEFINICIONES:
En un plano, dos rectas son paralelas si no tienen puntos comunes, o se confunden. Dos rectas del espacio son paralelas si están en un mismo plano y no tienen puntos comunes, o se confunden.

Se escribe: a || b.
Dos planos en el espacio son paralelos si no tienen puntos comunes o se confunden.
Se escribe a ê ê b .
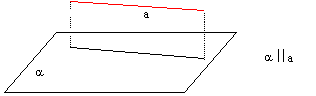
Una recta es paralela a un plano si hay una recta del plano que es paralela a la primera.
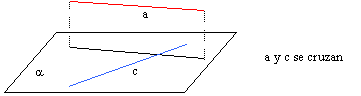
Dos rectas del espacio que no son paralelas y no tienen puntos en comun se dice que se cruzan.
Dos rectas de un plano, a y b, son perpendiculares si se cortan con un ángulo de 90o. Se indica así: a ^ b.
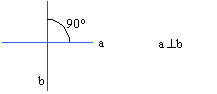
Una superficie reglada es la engendrada por una recta que se mueve sobre una curva. Pueden verse ejemplos en el tema cuerpos: cilindros y conos, paraboloide hiperbólico, hiperboloide de revolución, …
COMENTARIOS:
Hay líneas paralelas y perpendiculares en los paralelogramos; líneas y planos paralelos en los paralelepípedos,...
El cerebro de los seres humanos está particularmente dotado para percibir la perpendicularidad y, por tanto, el paralelismo, por la influencia de la gravedad.
En el arte y en la arquitectura hay abundantes ejemplos de paralelismo, que se traduce en verticalidad y horizontalidad de las líneas.
Con la regla y la escuadra podemos trazar paralelas y perpendiculares. Podemos pues transformar una figura en otra paralela, mediante una traslación, en la que la regla hace de guía y la escuadra de vehículo transportador:
RELACIONES:
V postulado de Euclides:
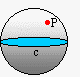
Por un punto exterior, P, a una recta, r, pasa una y sólo una recta, s, paralela a ella:

Nota: Obsérvese que en una esfera, dada una ‘recta’, c (una circunferencia máxima, por ser sus arcos la distancia mínima entre dos puntos) y un punto, P, de la esfera que no esté en la recta, no existen paralelas a la recta dada que pasen por el punto dado. Esto indica que la geometría de la esfera no es euclidiana.
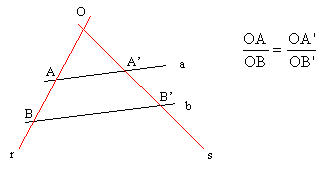
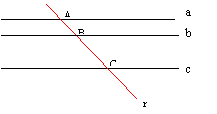
Teorema de Tales:
Si a, b y c son tres rectas paralelas de una plano y las cortamos por la recta r del mismo plano, la razón AB/AC es independiente de la recta r elegida.
Otra forma de enunciarlo: Los segmentos correspondientes que dos rectas paralelas a y determinan sobre otras dos rectas secantes r y s son proporcionales: