POLÍGONOS
DEFINICIONES:
Una línea poligonal es una sucesión finita de segmentos de un plano distintos y tales que el primero tiene un extremo común con el segundo; desde el segundo al penúltimo, cada segmento tiene un extremo común con el anterior y el otro extremo con el siguiente; finalmente, el último tiene un extremo común con el penúltimo.

Si el extremo libre del último segmento se une con el extremo libre del primero, la línea poligonal se llama cerrada.
Un polígono es una porción del plano limitada por una línea poligonal cerrada. Los segmentos de la línea poligonal se llaman lados del polígono. Los extremos de los lados se llaman vértices. Cada dos lados consecutivos determinan un ángulo del polígono.
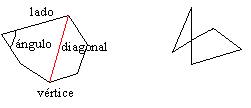
Se llama diagonal de un polígono a cualquier segmento de recta que una dos vértices que no sean consecutivos.
Clasificación:
Según el número de lados, los polígonos se denominan: triángulos, cuadriláteros, pentágonos, etc.
Si todos los lados del polígono son iguales, el polígono se denomina equilátero.
Si todos los ángulos son iguales, el polígono se llama equiángulo.
Los polígonos que son equiángulos y equiláteros se llaman regulares.
Si todos los vértices están en un mismo semiplano con relación a cualquier recta que contenga un lado del polígono, el polígono se denomina convexo. En caso contrario es cóncavo.

Construcción de polígonos en una circunferencia:
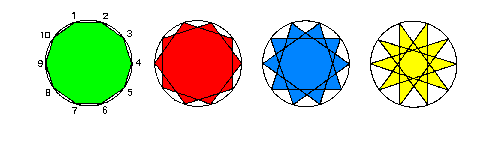
Si se señalan n puntos en una circunferencia, y se unen de manera consecutiva, se obtienen un polígono inscrito. Si los puntos determinan arcos iguales, el polígono será regular.
Si se unen los puntos de dos en dos, tres en tres, etc., se obtienen polígonos estrellados.
COMENTARIOS:
Polígono: del griego 'polys', numeroso + 'gonia', ángulo.
En la naturaleza puede observarse gran variedad de polígonos: flores, alas de insectos cristales, películas jabonosas, células, esqueletos de radiolarios, grietas ( por contracción de una placa),... El pentágono es tal vez la figura más abundante entre las flores.

RELACIONES:
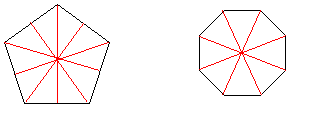
El ángulo central de un polígono regular de n lados es 360/n grados sexagesimales o, lo que es lo mismo, 2p /n radianes (ver la figura que sigue).
El ángulo de un polígono regular de n lados es (1-2/n)180 grados sexagesimales, es decir (1-2/n)2p radianes.
Un polígono regular tiene un alto grado de simetría: de n lados tiene n ejes de simetría y un centro de simetría.
En la tabla adjunta se resumen algunas de las características de los polígonos regulares:
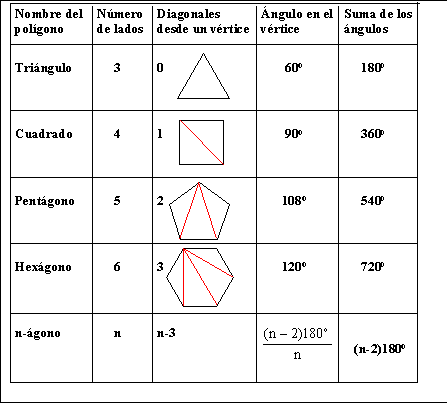
Algunos casos de polígonos estrellados:
Un polígono estrellado se obtiene uniendo mediante segmentos cada q vértices de los p vértices de un polígono. Para nombrarlos se utiliza el símbolo de L. Schlafli {p/q}.
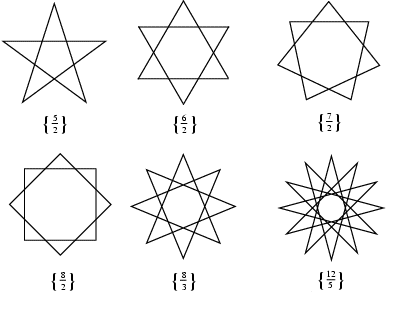
El dibujo de las diagonales de un polígono regular da lugar a bonitas figuras:
Cenefas (o frisos):
Una cenefa, o friso, es una figura plana obtenida por repetición de un motivo mínimo al que se le aplica una traslación a lo largo de una línea dada y simetrías respecto a un punto de dicha recta, o respecto a ejes paralelos o perpendiculares a la recta dada. Ejemplos:

Sólo existen 7 tipos de cenefas (prescindiendo del color), es decir 7 maneras esencialmente distintas de repetir un motivo en una franja:
| Diseños típicos | Transformaciones aplicadas |
| L L L L L L… | 1 traslación |
| L G L G L G … | 1 reflexión horizontal con deslizamiento |
| V V V V V V… | 2 reflexiones verticales |
| N N N N N … | 2 semigiros (giros de 180o) |
| V L V L V L … | 1 reflexión vertical y 1 semigiro |
| D D D D D D… | 1 traslación y 1 reflexión horizontal |
| H H H H H H … | 2 reflexiones verticales y 1 horizontal |
Un mosaico es un recubrimiento (sin huecos ni solapamientos) del plano con polígonos.
Mosaicos regulares: Son los que se obtienen con polígonos regulares iguales, uniendo lado con lado. Hay infinitos polígonos regulares, pero sólo con los de 3, 4 y 6 lados se puede rellenar el plano, sin dejar huecos.
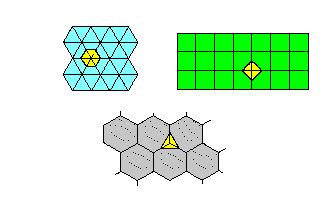
Sólo existen 17 tipos de mosaicos planos, si se utilizan simetrías y giros. Todos ellos pueden observarse en la Alhambra de Granada y en Aragón..
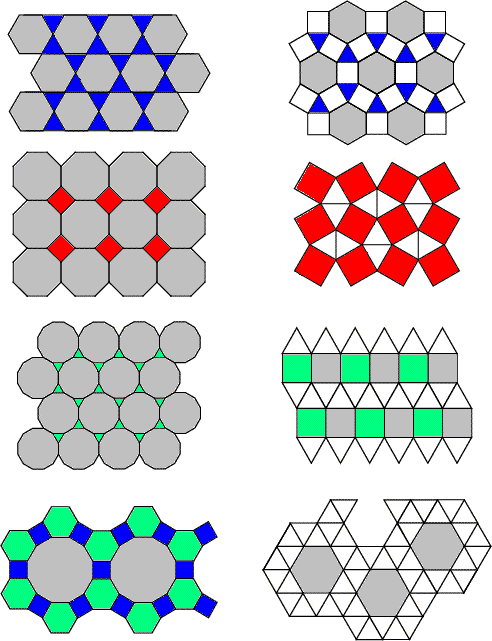
Mosaicos semirregulares: Si se mezclan polígonos regulares, se pueden construir ocho mosaicos semirregulares, de modo que los vértices sean todos similares
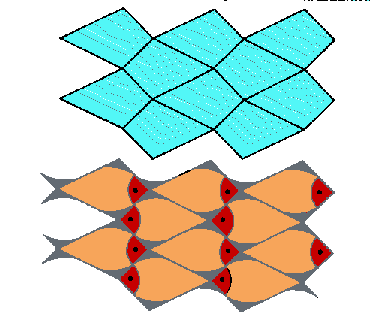
Por deformaciones de los polígonos, de modo que se conserve el área, se pueden construir mosaicos más variados. Así, a partir de mosaicos de cuadriltaeros, podemos construir este mosaico: