Juan Antonio Osuna  

Introducción a los Fractales:

• Historia y definición
• Características
• Visión práctica

Compresión Fractal de imágenes:

• Introducción
• Transformaciones afines
• Atractores
• IFS. Sistemas de Función Iterada
• Proceso de compresión
• Proceso de descompresión
• Características más reseñables

Links sobre Compresion Fractal de imágenes

Introducción a los Fractales

Hoy en día, después de que en 1975 Benoit Mandelbrot acuñara la palabra fractal, 21 años después no existe una definición generalizada del mismo. A pesar de esto, tomando como base el conjunto de Mandelbrot podemos aproximar una definición:

Un Fractal, palabra que proviene del latín 'fractus' o lo que es lo mismo, algo roto, algo no entero, comprende objetos geométricos de cierta entidad que pueden ser descritas en términos de dimensiones no enteras o dimensiones fractales.

Las características que definen un fractal son las siguientes:

• Autosimilitud: A diferentes escalas, un fractal conserva la misma apariencia, siempre existe una clara similitud entre partes muy distantes de una misma figura fractal.
• Infinito Detalle: Relacionada con la anterior característica, al ampliar un fractal, tanto más detalle revela este, sin que se tenga un límite en el que se aprecien bloques.
• Dimensión no entera: Al contrario de la geometría clásica, en la que la las figuras tienen 1, 2 o 3 dimensiones, un fractal puede desarrollarse en una dimensión no entera, como, por ejemplo la curva de Koch, que lo hace en la dimensión 1.26; esto es, ocupa parte del plano pero no llega a tener la entidad de figura bi-dimensional.

Desarrollo de la curva de Koch

• Las fórmulas o algoritmos que los definen son relativamente sencillos y con un conjunto muy reducido de datos.
• Su algorítmia es definida por una característica clave: la iteración. Es gracias precisamente al ordenador lo que permite experimentar y descubrir nuevos conjuntos y sin él, probablemente Mandelbrot no hubiese llegado tan lejos. El ordenador fué y es imprescindible en cualquier campo que abarque los fractales.

Además de la belleza plástica que todos hemos contemplado en la generación de un fractal, es algo más que bellas e intrincadas imágenes generadas por ordenador; en la última década los fractales se utilizan para la representación y el análisis de una gran variedad de procesos complejos a lo largo de diversos campos, como pueden ser la Física, las Matemáticas, Biología, Química, Geología, ....

La facilidad de los fractales para expresar o simular fenómenos que suceden en la Naturaleza es debido a la autosimilud; los fenómenos naturales creados o en los que interviene el azar, la aleatoriedad, estadísticamente siguen una periodicidad o autosimilitud que puede ser caracterizada a través de la dimensión fractal.

La utilización de la geometría fractal en investigaciones numéricas, teóricas y experimentales, ha hecho posible tener una visión práctica y predecible de problemas que antes eran prácticamente intratables.

Compresión Fractal de imágenes

Una de las aplicaciones más excitantes a través de los fractales y su aplicación en el mundo de las imágenes digitales es sin duda la Compresión Fractal de imágenes. A continuación se expresa una pequeña introducción a la compresión Fractal:

En 1987 Michael Barnsley, fundador de la empresa Iterated Systems junto con Alan Sloan, descubrió que era posible controlar el contenido de una imagen fractal de forma precisa y hacerla parecer increíblemente similar a una imagen del mundo real. Un ejemplo temprano de aproximación a una imagen real basado en fractales lo contituye el clásico helecho fractal.

El helecho completo mantiene una apariencia similar en cada una de sus hojas, cada hoja con sus sub-hojas y así sucesivamente. Sigue un patrón claramente definido.

La generación de la anterior figura proviene, en su base, de un simple sistema de ecuaciones que opera en el plano a través de rotaciones, traslaciones y escalados; se trata de la transformación afín y constituye parte fundamental de la compresión fractal. Expresada en términos numéricos, no son más que los coeficientes del sistema de ecuaciones anteriormente citado, y por ello su sencillez y su capacidad de compresión. El conjunto de estos coeficientes constituye lo que se llama mapa de afinidad. 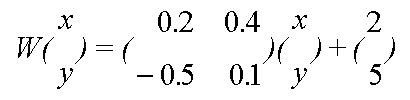Transformación afín expresada de forma matricial.

Concretando sobre la compresión fractal, esta se basa en un tipo concreto de transformación afín: las transformaciones afines contractivas y se caracterízan porque su resultado en el plano euclídeo es más pequeño que la imagen a la que se le aplicó la transformación afín (matemáticamente, la distancia entre dos puntos cualesquiera de la imagen original es siempre mayor o igual que la distancia entre ambos puntos tras haberles aplicado la transformación afín contractiva).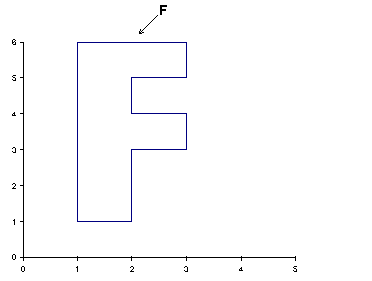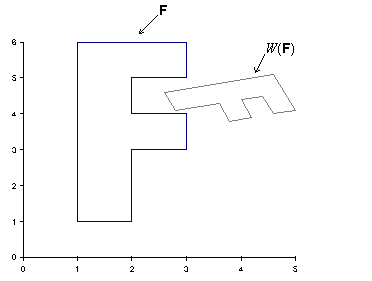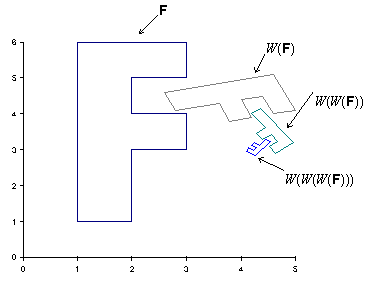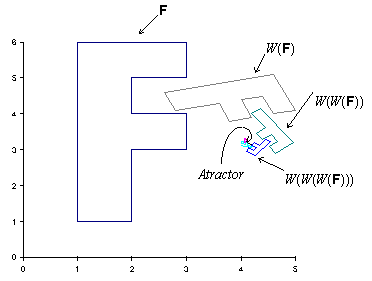

Si observamos la imagen anterior, el mapa de afinidad W converge a un punto fijo. Este fenómeno sucede con todas las transformaciones afines contractivas, y el punto o puntos fijos recibe el nombre de atractor. El atractor, independientemente de la imagen de origen es siempre el mismo.

Un grupo de transformaciones afines contractivas que actúan en conjunto sobre el plano constituyen los llamados Sistemas de función Iterada o IFS. En los IFS sucede lo mismo que con una transformación afín y su atractor. Cualquier imagen a la que se le aplique el IFS, conduce siempre a una misma figura o atractor (en este caso, ya no se trata de un punto, si no de una figura definida). Proceso de obtención del atractor para el helecho fractal

Para definir la imagen del helecho fractal tan solo son necesarias 24 bytes que es lo que ocupan los mapas de afinidad de las 4 transformaciones afines que contituyen el IFS generador del helecho.

Aunque tan solo intuitivamente, ya observamos el poder de compresión por parte de los IFS, aunque tan solo sea en blanco y negro y para una imagen no-arbitraria (el helecho).

Pero, ¿¿ Como hallar las transformaciones afines que definen una imagen del mundo real ??. La búsqueda de un IFS que defina a toda una imagen dada es una utopía. Es necesario utilizar lo que se llama el proceso de Transformación Fractal, que busca las redundancias dentro de la propia imagen a través del mapeado con IFS locales ( que no son más que los IFS normales, salvo que, en lugar de actuar sobre todo el plano que define a la imagen, actúan solamente sobre la parte 'redundada', sobre una parte limitada de la imagen, de ahí el nombre de 'locales').
 

Básicamente, el proceso de compresión, muy a grandes rasgos, es el siguiente:

• La imagen origen es dividida en subconjuntos llamados regiones de dominio, sobre las que se buscarán redundancias dentro de la imagen.
• Para cada región de dominio se escoge una región de rango, mayor en tamaño que la región de dominio.
• Todas las posibles regiones de rango sin rotadas, escaladas y se las aplica una simetría (en definitiva, una transformación afín), eligiendo la región de rango que junto con la transformación afín mas se aproxime a la región de dominio.
• La elección de la región de rango, junto con la transformación afín, se almacenan en el fichero fractal, y contituirán los patrones para la descompresión y así reconstruir la imagen original.

El proceso de descompresión se resume en iterar un número suficiente de veces todas las transformaciones afines almacenadas sobre las regiones de rango hasta llegar a un conjunto invariante, al atractor, que es una buena aproximación de la imagen original (al tratarse de una compresión con pérdidas, nunca será una réplica pixel a pixel del original).

Proceso de descompresión de una imagen fractal

Características de la compresión Fractal: Ventajas y desventajas

• Tecnología de 'compresión con pérdidas' de reciente creación y superior al método JPEG.
• Sujeta a una patente comercial, perteneciente a Iterated Systems. A pesar de ello, Iterated Systems ofrece un gran aperturismo a través de Internet, intentando alcanzar que esta tecnología se convierta en un estandar 'de hecho'
• Zoom avanzado sin pixelización. Al ser independiente de la resolución, no produce la aparición de bloques ampliados (pixels). A pesar de ello, la ampliación no deja de ser una forma avanzada de interpolación.
• Ahorro de espacio de almacenamiento y, evidentemente, menores tiempos de transmisión de imágenes a través de Internet.
• El proceso de Compresión/Descompresión es acentuadamente asimétrico. Mientras que la descompresión es casi inmediata, la compresión requiere considerablemente más tiempo de computación.