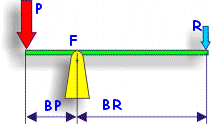
Con los cuatro elementos tecnológicos de una palanca se elabora la denominada Ley de la palanca, que dice :
La "potencia" por su brazo es igual a la "resistencia" por el suyo.
Ley de la palanca |
Descripción Utilidad |
 |
Con los cuatro elementos tecnológicos de una palanca se elabora la denominada Ley de la palanca, que dice : La "potencia" por su brazo es igual a la "resistencia" por el suyo. |
Matemáticamente se puede poner:
POTENCIA x BRAZO DE POTENCIA = RESISTENCIA x BRAZO DE RESISTENCIA |
|
P x BP = R x BR |
Esta expresión matemática representa una proporción inversa entre la "potencia" y su brazo por un lado y la "resistencia" y el suyo por el otro. Por tanto, para una "resistencia" dada, aumentos de la "potencia" obligan a disminuir su brazo, mientras que aumentos del brazo de potencia supondrán disminuciones de su intensidad.
Por esta razón es lo mismo emplear una potencia de 8 N y un brazo de potencia de 0,25 m, que una "potencia" de 0,5 N y un brazo de potencia de 4 m, pues su producto es equivalente. Algunas otras posibilidades las podemos ver en la tabla siguiente:
| P (Potencia en Newton) | BP (Brazo de Potencia en metros) | PxBP |
| 8 | 0,25 | 2 |
| 2 | 1 | 2 |
1 |
2 |
2 |
| 0,5 | 4 | 2 |
Esta expresión matemática podemos sentirla de forma práctica si pensamos en estos ejemplos:
La fuerza necesaria para hacer girar una puerta (potencia) es menor cuanto más lejos de las bisagras (brazo de potencia) la aplicamos.
Es mas facil cortar una alambre (potencia) con unos alicates de corte, cuanto mas cerca del eje lo colocamos (brazo de resistencia) y cuanto más lejos de él aplicamos la fuerza (brazo de potencia).
Al emplear un cascanueces es más fácil romper la nuez (resistencia) cuanto más lejos (brazo de potencia) ejerzamos la fuerza (potencia).
Si en vez de considerar la intensidad de las fuerzas de la "potencia" y la "resistencia" consideramos su desplazamiento, esta ley la podemos enunciar de la forma siguiente: El desplazamiento de la "potencia" es a su brazo como el de la "resistencia" al suyo. |
|
expresión que matemáticamente toma la forma:
Esto representa una proporción directa entre el desplazamiento de la potencia y su brazo, de tal forma que para aumentar (o disminuir) el desplazamiento de la potencia es necesario también aumentar (o disminuir) su brazo, y lo mismo sucedería con la resistencia.
Estas expresiones permite determinar los elementos tecnológicos de las palancas para solucionar los problemas técnicos planteados.
©2005 CEJAROSU |
MecanESO |