| Unidad 1 | Actividad 5 |
|---|
Actividad 5. Mitad y Mitad
Propósito
Compararás fracciones mayores, iguales y menores a un medio.
¿De cuántas formas diferentes se podrá comprar |
|---|
Algunas regiones de nuestro país son grandes productoras de miel, como Campeche, Chiapas, Quintana Roo, Tabasco y Yucatán, este último como el líder nacional. La miel se vende en frascos de un litro, de ![]() litro y de
litro y de ![]() de litro.
de litro.
| 1. | Presiona el botón Recursos, y a continuación en Revista, lee “Ñati y su grupo”, y responde las preguntas siguientes. |
|---|

| A) | ¿Cuáles de las ideas siguientes son ciertas con respecto a la lectura de "Ñati y su grupo"? |
|---|
| I | Los acajay estaban preocupados porque necesitaban un sistema de equivalencias de fracciones que fuera fácil de comprender. |
|
|---|---|---|
| II | ||
| III | ||
| IV | ||
| V |
| Inténtalo de nuevo |
|---|
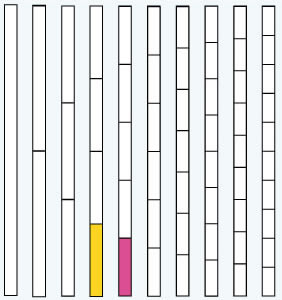
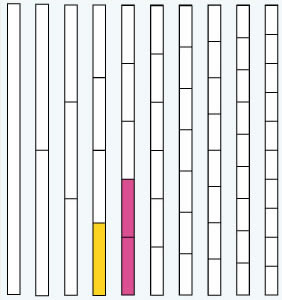
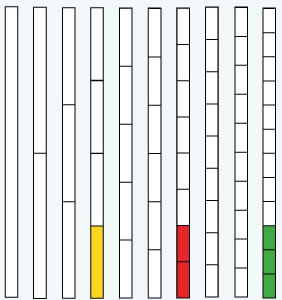
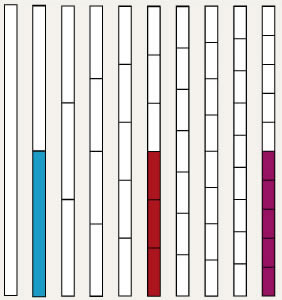
| 2. | Observa la vara blanca de los acajay y el juego de medidas que creaste con las tiras, y responde las preguntas siguientes. |
|---|
| A) | ¿Es posible medir con exactitud una tira de |
|---|
| Inténtalo de nuevo |
|---|
En caso de ser afirmativa tu respuesta, escribe la medida correspondiente.
| B) | ¿Es posible medir con exactitud una tira de |
|---|
| Inténtalo de nuevo |
|---|
En caso de ser afirmativa tu respuesta, escribe la medida correspondiente.
| C) | ¿Es posible medir con exactitud una tira de |
|---|
| Inténtalo de nuevo |
|---|
En caso de ser afirmativa tu respuesta, escribe la medida correspondiente.
| D) | ¿Es posible medir con exactitud una tira de |
|---|
| Inténtalo de nuevo |
|---|
En caso de ser afirmativa tu respuesta, escribe la medida correspondiente.
| E) | ¿Es posible medir con exactitud una tira de |
|---|
| Inténtalo de nuevo |
|---|
En caso de ser afirmativa tu respuesta, escribe la medida correspondiente.
| 3. | Observa el diagrama siguiente y completa la serie de equivalencias. | |
|---|---|---|
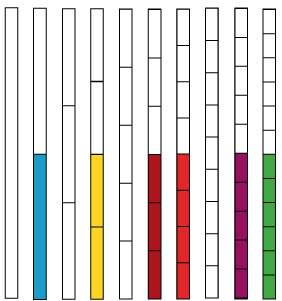
| 4. | Oprime el botón Diagrama y utilízalo para completar las equivalencias. Haz clic en la primera fracción de cada ejercicio, después oprime el botón Equivalencias y completa. |
|---|
¡Reflexiona tu respuesta!
¡Muy Bien! |
|||||||||||
Lee el diálogo entre Susana y Rosa con respecto a cómo encontrar las equivalencias de un ![]() .
.
Resolvamos otros problemas
| 5. | Obtén otras equivalencias. Oprime el botón Diagrama, señala la fracción haciendo clic en las partes de la tira correspondiente y después busca las fracciones equivalentes, haciendo también clic sobre las partes de las otras tiras. Escribe en los cuadros las equivalencias obtenidas. Si te equivocas haz clic en el botón Limpiar tira. | |
|---|---|---|
¡Reflexiona tu respuesta!
¡Muy Bien! |
||||||||
¡Reflexiona tu respuesta!
¡Muy Bien! |
¡Reflexiona tu respuesta!
¡Muy Bien! |
| 6. | Escribe dos fracciones que no tengan alguna equivalencia en este diagrama. |
|---|
| 7. | Compara las fracciones siguientes, y selecciona el símbolo > “mayor que” o |
|---|
< |
>
| = |
| 8. | Roberto compró dos cables del mismo tamaño para instalar dos lámparas. La primera fue una lámpara de techo para la cual utilizó |
|---|
| A) | ¿Cuál de las afirmaciones siguientes es correcta con respecto a la situación anterior? |
|---|
| Inténtalo de nuevo |
|---|
| 9. | Abigail y Damiana compraron tela para hacerse unas blusas. Los pedazos de tela que compró cada una fueron del mismo tamaño. Abigail utilizó |
|---|
| A) | ¿Cuál de las afirmaciones siguientes es correcta con respecto a la situación anterior? |
|---|
| Inténtalo de nuevo |
|---|