PIRÁMIDE REGULAR
|
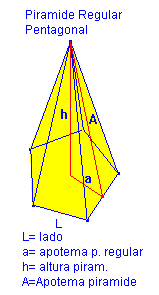
La figura muestra una pirámide regular y su
desarrollo, que nos permite deducir el área.
Como vemos en la figura:
Área lateral = N · Área Triángulo
Siendo N el número de lados del polígono que forma la base. |
|
ÁREA Y VOLUMEN DE UNA PIRÁMIDE
|
 |
Á Total = A Lateral + A Base
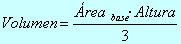
Base = Polígono Regular.
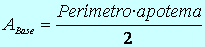

No confundas apotema
del polígono con apotema de la pirámide (=altura triángulo de una cara) |
Ejercicios
|
1.-Observa en la figura los cálculos realizados para calcular
área y volumen.
Mueve los
puntos marcados en la pirámide para que:
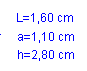
a) Calcula A
aplicando el teorema Pitágoras.
|
|
2.- Calcula el
área y el volumen de una pirámide cuadrangular de igual lado y altura.
CONO
La figura muestra el desarrollo de un cono, un sector circular y una
circunferencia.
|
La longitud de la circunferencia, 2Πr,
es igual a
la longitud del arco del sector 2Πgn/360.
2Πr=2Πgn/360, de donde
n=360r/g.
Luego el área lateral es A L=Πrg
y el área total es:
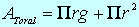
|
|
Ejercicios:
1.-Modifica el cono para que el ángulo del sector
circular sea recto (puede que exacto no lo consigas) ¿Que relación hay
entre la generatriz y el radio?
2.-Calcula el área de un
cono de radio 1,3 m y generatriz 3,6 m. ¿Cuánto mide la altura del cono?
ÁREA Y VOLUMEN DEL CONO
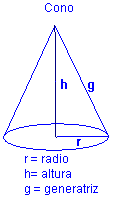 |
Á.Total = A.Lateral + A.Base
Volumen = A.Base · Altura / 3
Base = Círculo,
Circunferencia
A Base=
Π r2
A Lateral
= Π·r·g
V=Π·r2·h / 3
|
|
ESFERA
Como ya sabes no es posible hacer el desarrollo de una esfera.
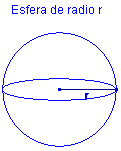 |
ÁREA DE LA ESFERA
A= 4·Π·r2
VOLUMEN
V= 4/3
Π ·r3 |
|
Calcula el área y volumen de una esfera de radio 2 cm. Si haces el radio
el doble, ¿cuánto aumenta el área? ¿y el volumen? comprueba tus cálculos
en el grafico. Puedes mover la
circunferencia exterior.
|
|
|