
FRACTALES
DEFINICIONES:
Fractal procede del adjetivo latino 'fractus', que significa interrumpido" o irregular. La geometría fractal es un lenguaje creado por Benoît Mandelbrot en 1975 para describir las formas complejas de la naturaleza, como nubes, sistemas montañosos, galaxias, flores, ramificaciones arboreas y bronquiales, rocas, cuencas hidrográficas, sistema neuronal, las líneas costeras, esponjas, ...
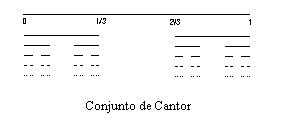
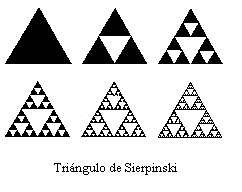
y objetos matemáticos como el conjunto de Cantor o el triángulo de Sierpinski, cuyo comportamiento caía fuera del marco de la matemática tradicional.
Para describir los fractales se utilizan principalmente algoritmos y no las formas básicas de la geometría tradicional, como punto, recta y plano.
Se suelen distinguir dos tipos de objetos fractales: deterministas y aleatorios.
Objetos fractales deterministas:
La descripción de estas formas se realiza por la relación entre sus partes. Se caracterizan por la autosemejanza de algunas de sus partes con el todo. Es decir que partes del objeto son pequeñas replicas del total. En cada escala, se repite un motivo geométrico. Un objeto es estrictamente autosimilar o sibisemejante si puede descomponerse en partes que son replicas exactas del total. Cualquier parte arbitraria contiene una replica exacta del objeto total.
Para dibujar un fractal, debemos partir de una figura básica (un segmento, por ejemplo) y aplicar repetidamente los algoritmos definidos. Este proceso, es infinito. La figura limite resultante es un fractal.
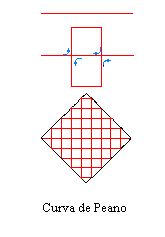
Ejemplos: Además del conjunto de Cantor y del triángulo de Sierpinski, antes citados, se pueden añadir, entre una infinidad, la curva de Peano y la de Koch. En estos casos, los objetos se construyen por un proceso recursivo de cambio de escala (reducida) y sustitución multiplicativa, de modo que el factor de reducción de escala s y el número de piezas sustituidas son siempre los mismos. La iteración de diversas transformaciones geométricas aplicadas a un objeto arbitrario conduce a figuras fractales similares a fotografías de objetos reales como nubes, helechos, montañas, paisajes,...
Objetos fractales aleatorios:
Aquí se introducen variaciones aleatorias en el proceso de construcción mediante el algoritmo. Sin embargo, en cualquier escala, los detalles parecen ser invariantes. Figuras aparentemente complejas de la naturaleza, si se analizan a distintas escalas, presentan siempre los mismos algoritmos básicos de construcción.
Ejemplos: Montañas, costas, ramificaciones bronquiales, …
Dimensiones fractales:
Para medir la complejidad de una figura, es decir el grado de irregularidad y de interrupción de los fractales se generaliza el concepto habitual de dimensión espacial, y se define la dimensión fractal como grado de ocupación del espacio: Un punto tiene dimensión 0; una línea tiene dimensión 1; un plano, dimensión 2; una bola, dimensión 3; … El conjunto de Cantor ocupa más que un punto, pero menos que una linea, con lo que su dimensión debería estar entre 0 y 1; el triángulo de Sierpinski y la de Koch ocupan más que una línea, pero no todo el plano, con lo que su dimensión debería estar entre 1 y 2; la curva de Peano puede demostrarse que ocupa todo el plano, su dimensión debería ser 2; …
Ver el apartado relaciones para obtener más detalles sobre la dimensión fractal..
COMENTARIOS:
Un fractal es un objeto que, si lo ampliamos, va mostrando una estructura similar. Los fractales son simétricos respecto a cambios de escala.
Hay una estrecha relación entre los fractales y el crecimiento: La geometría fractal es la geometría de los procesos caóticos; es decir de los procesos dinámicos cuyo desarrollo depende crucialmente de las condiciones iniciales. No todos los objetos de la naturaleza son fractales, pero tienen una alta probabilidad de formarse.
Una de las aplicaciones de la teoría de los fractales es el tratamiento de las imágenes digitales: Se descompone la imagen en unos pocos subconjuntos. Cada uno de estos se representa por un conjunto de algoritmos cuya aplicación lo reproduce, de manera aproximada. Así hay un enorme ahorro en la transmisión de imágenes.
RELACIONES:
Veamos algunos modos de definir la dimensión fractal, utilizando los resultados del caso entero
Dimensiones fractales:
Sea s un factor de reducción de escala.
Dimensión de sibisemejanza: Si dividimos en 1/s partes cada una de las dimensiones de un segmento, un cuadrado, un cubo, … el número, N, de elementos análogos, pero a menor escala, que resultan viene dado por la expresión N=(1/s) D, siendo D la dimensión espacial en cada caso. Tomando logaritmos en ambos miembros y despejando D se obtiene (ver tabla adjunta):
Factor de reducción de escala s |
Nº de elementos N |
Ley potencial N=(1/s) D |
Dimensión D=logN/log(1/s) |
|
| Segmento | 1/3 |
3 |
3=31 |
1=log3/log3 |
| Cuadrado | 1/3 |
9 |
9=32 |
2=log9/log3 |
| Cubo | 1/3 |
27 |
27=33 |
3=log27/log3 |
Aplicando esta misma relación al caso de los fractales sibisemejantes, N es el número de piezas que se reemplazan en cada paso de la construcción y s el factor de escala, se obtiene que: el conjunto de Cantor tiene dimensión 0,631; la curva de Peano tiene dimensión 2 y la de Koch 1,262 y el triángulo de Sierpinski 1,585 (ver tabla adjunta)
Factor de escala s |
Nº de elementos N |
Ley potencial N=(1/s)D |
Dimensión D=logN/logs |
|
| Conjunto de Cantor | 1/3 |
2 |
2=3D |
D=log2/log3=0,631 |
| Curva de Koch | 1/3 |
4 |
4=3D |
D=log4/log3=1,262 |
| Curva de Peano | 1/3 |
9 |
9=3D |
D=log9/log3=2 |
| Triángulo de Sierpinski | ½ |
3 |
3=2D |
D=log3/log2=1,585 |
Dimensión de caja: Se cubre el fractal con una retícula cuadrada en el plano (cúbica, si es en el espacio) y se cuenta el número N de cuadrados (cubos) que contienen puntos del fractal. Se procede del mismo modo con reticulas cuyo lado sea la mitad que las anteriores. Idem con retículas cuyo lado sea la fracción s del de la primera.
Se dibujan los puntos (log N, log(1/s)), para distintos valores de s, en una hoja doblemente logaritmica, y se ajusta la recta a la nube de puntos resultante. La pendiente de esta recta representa la dimensión de caja.
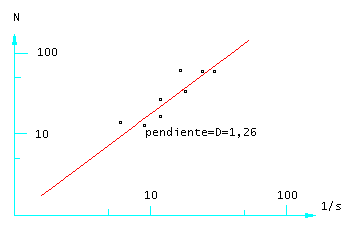
Así pues, según el procedimiento adoptado, se tendrá un definición u otra de dimensión fractal que, en general, no serán coincidentes.