|
Georges Louis Leclerc(1707-88), Conde de Buffon
fue un celebre naturalista francés autor de una monumental Historia Natural
en 44 tomos que recopilaba el conocimiento científico con un fin
eminentemente divulgativo. Hoy en día su nombre aparece muchas veces asociado
a un problema denominado "La aguja de Buffon" que relaciona el número
pi con el lanzamiento de una aguja sobre una superficie rayada.
Buffon demostro que si lanzamos, al azar, una aguja de longitud L sobre
una superficie en la que hay dibujadas líneas paralelas separadas una
distancia D, la probabilidad de que la aguja corte a una línea es :
Vamos a utilizar este resultado para medir 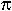
Material Necesario
- Una superficie con líneas paralelas (Puede servir
una hoja de papel sobre la que previamente hayas dibujado varias líneas equidistantes o un suelo embaldosado)
- Una aguja, palillo u objeto similar, de longitud
menor o igual a la distancia entre líneas (Para simplificar es
conveniente que la distancia entre dos rayas coincida con la longitud de
la aguja)
Método

- Deja caer, de la forma más aleatoria posible, la
aguja sobre la superficie.
- Anota el número de tiradas y el número de veces que
la aguja corta a una línea.
- El cociente entre el número total de tiradas y el número
de veces que la aguja corta a una línea tiende a pi/2 ( se parecerá
tanto más cuanto mayor sea el número de tiradas)

- Si la aguja tiene una longitud (L) menor que
la distancia entre dos líneas (D) :

Aquí tienes dos programas para simular el experimento
de la aguja de Buffon en tu ordenador :
Si quieres conocer unas cuantas cifras
de Pi
Si quieres saber un poco más sobre el número Pi: el
número 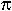
 Más
experimentos Más
experimentos
|
