Algunas curiosidades sobre el número Pi ()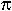

• Pi es la razón de la circunferencia de un circulo a su diámetro
  
  
• En distintas culturas, china, egipcia, europea, india, etc., se trato de obtener mejores aproximaciones de Pi por ser de aplicación en campos tan distintos como la astronomía o la construcción.
  
  
• Muchos de los intentos de evaluar Pi en la antigüedad utilizaban el método de calcular el perímetro de polígonos inscritos y circunscritos a circunferencias.
  
  
• Modernamente para evaluar Pi se utiliza una serie infinita convergente. Este método fue utilizado por primera vez en Kerala (India) en el Siglo XV
  
  
• La probabilidad de que dos enteros positivos escogidos al azar sean primos entre si es 6/Pi²
  
  
• Si se eligen al azar dos números positivos menores que 1, la probabilidad de que junto con el número 1 puedan ser los lados de un triángulo obtusángulo es (Pi-2)/4
  
  
• En 1706, el inglés William Jones fue el primero en utilizar el símbolo griego 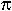para denotar la relación entre la circunferencia y su diámetro. Euler en su obra "Introducción al cálculo infinitesimal", publicada en 1748, le dio el espaldarazo definitivo.
  
  
• Muchos intentos para determinar Pi con exactitud están relacionados con el clásico problema de la cuadratura del círculo : "construir, utilizando únicamente regla y compás, un cuadrado de área igual a un círculo dado".
  
  
• Johan Heinrich Lambert(1728-1777), matemático alemán, probó que Pi es irracional. ( Un número irracional no se puede escribir en forma de fracción racional. Números racionales son : 1, 2 , 3/4, 17/23)
  
  
• Ferdinand Lindemann(1852-1939) demostró que Pi es un número trascendental. Esto significa entre otras cosas que el problema de la cuadratura del círculo no tiene solución. Pese a ello todavía se sigue intentando.
  
  

  Algunos valores de Pi obtenidos antes de 1600

  Matemático o Lugar	año	valor
  La Biblia (Reyes-I-7-23)		3
  Papiro de Ahmes (Egipto)	1650 a.C.	3,16
  Tablilla de Susa (Babilonia)	1600 a.C.	3,125
  Bandhayana (India)	500 a.C.	3,09
  Arquímedes de Siracusa	(287-212 a.C)	entre 223/71 y 220/70
  Liu Hui (China)	260	3,1416
  Tsu Chung Chih	480	Entre : 3,145926 y 3,1415927
  Al-Kashi (Persia)	1429	3,1415926535897932
  Franciscus Vieta (Francia)	(1540-1603)	3,1415926536

  
  
  
• El matemático alemán Ludolph van Ceulen(1540-1610) pidió que, como epitafio, escribiesen en su lápida las 35 cifras del número Pi que había calculado. Los alemanes llaman a Pi el número ludofiano.
  
  
• William Shanks, matemático inglés, dedico 20 años de su vida a la obtención de 707 decimales de Pi.(En 1945 se descubrió que había cometido un error en el decimal 528 y a partir de este todos los demás eran incorrectos)
  
  
• En 1949 uno de los primeros ordenadores el ENIAC, trabajando durante 70 horas, determino Pi con 2037 decimales.
  
  
• En 1959, ordenadores en Francia e Inglaterra calcularon más de 10.000 cifras de Pi.
  
  
• En 1961 Daniell Shanks(sin relación con William Shanks) y Wrench, obtuvieron en 8 h 23 min, 100.265 cifras en un IBM 7090.
  
  
• En 1983, Yoshiaki Tamura y Yasumasa Kanada, en menos de 30 h, en un HITAC M-280 H obtuvieron 16.777.206 (2²⁴) cifras.
  
  
• En Julio de 1997, Yasumasa Kanada y Daisuke Takahashi obtuvieron 51.539.600.000 cifras , utilizando un HITACHI SR2201 con 1024 procesadores.
  
  
• Programas para simular el problema de la aguja de Buffon: Buffon (DOS) (9 kbytes), Buffon (Windows 95)(143 kbytes)
  
  
• Si quieres conocer unas cuantas cifras de Pi
  
  
• Busca tu número de teléfono en las 50.000.000 primeras cifras de Pi
  
  
• Una página con mucha información sobre Pi (en inglés)
  
  
• Página de enlaces sobre Pi (en inglés)
  
  
• Simon Newcomb, astrónomo y matemático americano, dijo en una ocasión que treinta cifras decimales de Pi darían la circunferencia del universo visible hasta una cantidad que sería imperceptible incluso con el más potente telescopio.

Más curiosidades