
 |
Cuerpos de revolución |
| Primer Ciclo de Educación Secundaria Obligatoria | |
| Curiosidad. Correspondencia del área de la superficie esférica y el área lateral del cilindro. Zona esférica. |
||
| Se llama zona esférica a la superficie esférica comprendida entre dos planos paralelos. | ||
| |
Arquímedes descubrió que si los seccionamos horizontalmente por dos planos paralelos, el área de la zona esférica es igual a la correspondiente en la superficie lateral del cilindro.
Para demostrarlo vamos a
considerar una franja muy estrecha. |
|
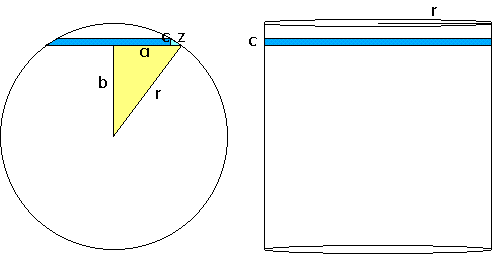 |
Los triángulos
rectángulos de color azul claro y amarillo son semejantes porque
sus hipotenusas son respectivamente perpendiculares, igualmente lo son
sus catetos. Sus ángulos son iguales y sus lados proporcionales.
Consideremos la razón hipotenusa/cateto menor r/a = z/c Producto de medios = producto de extremos a · z = r · c Para hallar la superficie de una banda, al ser muy estrecha nos basta multiplicar longitud de su circunferencia · ancho Área de la banda de zona esférica = 2 · π · a · z Área de la banda de superficie lateral de cilindro = 2 · π · r · c Observa los factores de estas ecuaciones y los de la igualdad anterior. Basándote en esto deduce la ecuación del área de la zona esférica , conociendo los datos del radio de la esfera y la distancia de separación de los planos que la limitan. |
|
| Eduardo Barbero Corral | ||
 |
||
| ProyectoDescartes.org. Año 2005 | ||
![]()
Los contenidos de
esta unidad didáctica están bajo una licencia
de Creative Commons si no se indica lo contrario.