Cuerpos de revolución
Primer Ciclo de Educación Secundaria Obligatoria
 

Curiosidad.
La suma del área de la sección de la esfera y la del cono doble es igual a la del cilindro.
En la imagen tenemos una esfera, un doble cono y un cilindro. Todos tienen el mismo radio, la altura de cada cono es igual al radio, y la altura del cilindro es igual al diámetro. Arquímedes descubrió que si les seccionamos por un plano horizontalmente el área de la sección de la esfera más la del cono es igual a la del cilindro.
 

Pica sobre los triángulos de abajo o mantenlos presionados varios segundos para subir o bajar el plano que secciona las figuras.

r es el radio en las tres figuras.
a es el radio de la sección en la esfera.
b es la distancia en vertical al centro.
En este cono se cumple que el radio de su sección coincide con la distancia al centro, ya que la inclinación de la generatriz es 45º

Área de la sección de la esfera = π · a2

Área de la sección del cono = π · b2

Área de la sección del cilindro = π · r2

Si sumamos las dos expresiones primeras y aplicamos el teorema de Pitágoras en el triángulo rectángulo de la primera figura
π · a2 + π · b2 = π · (a2 + b2 ) = π · r2

Esto también demuestra que el volumen de la esfera más el volumen de los conos es igual al volumen del cilindro.


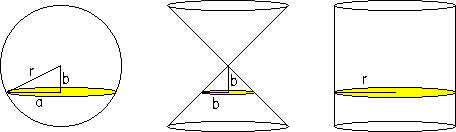Basándote en ello deduce la ecuación del volumen de la esfera.
Esta propiedad también nos aporta un método para hallar el volumen de un segmento esférico. El segmento esférico es la parte de esfera que está entre dos planos paralelos. Para hallar su volumen nos bastaría hallar el volumen de la parte correspondiente de cilindro y restarle la parte correspondiente de los conos.
         
           
  Eduardo Barbero Corral
 
ProyectoDescartes.org. Año 2005
 
 

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.