|
Edificios es un problema lógico clásico cuyo planteo es el siguiente: en un tablero cuadrado de n x n hay que colocar números de 1 a n; en cada casilla va exactamente un número y no puede haber dos números iguales en una misma fila o columna. Alrededor del tablero hay pistas que indican cómo deben ser colocados esos números, para entenderlas hay que imaginar que cada uno de los números a colocar representa la altura de un edificio; las pistas nos dicen cuántos edificios ve una persona que esté parada en esa posición si se coloca mirando hacia el tablero, bajo la suposición de que cada edificio oculta a todos los que estén detrás de él y que sean a la vez más bajos que él, pero que no oculta a los que sean más altos.
Un ejemplo con su solución:
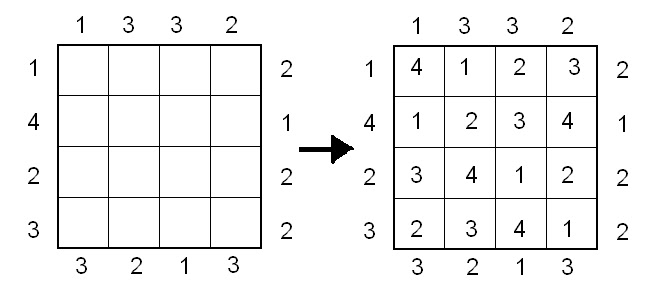
Una de las condiciones que todo buen problema de lógica debe cumplir es que su solución sea única, es decir, no puede haber dos formas diferentes de completar el tablero respetando a la vez todas las pistas. A veces sucede que este objetivo se logra con una cantidad menor de pistas. Por ejemplo, en el problema anterior hay, en efecto, pistas redundantes (véase http://eltopologico.blogspot.com/2013/02/edificios.html).
Las dos escenas son tomadas del Proyecto Canals. |


![]()