Casos prácticos
Caso práctico 1. Suma, multiplicación, fracciones y agrupamientos
La fórmula a construir es:
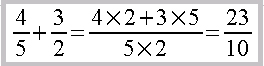
Pasos a seguir:
-
La fórmula es una igualdad doble, por tanto, desde el cuadro Elementos, en el tipo Relaciones pulsa dos veces sobre el símbolo a=b (Es igual). En el documento se empezará a escribir la fórmula y en la ventana de comandos irá apareciendo la codificación de la fórmula en el lenguaje de LibreOffice Math. Después de este primer paso, aparecerán así:
-
En el documento:

- En la ventana de comandos: <?> = <?> = <?>
-
En el documento:
- El término izquierdo de la igualdad es una suma, por tanto selecciónalo (haz doble clic sobre el cuadradito que lo representa para que aparezca resaltado en la ventana de órdenes o selecciónalo directamente en dicha ventana) y en el grupo Operadores unarios/binarios aplica a+b (+ de suma).
- Cada sumando es una fracción, por tanto selecciónalos sucesivamente y aplica a cada uno el operador de División (fracción).
- Ya tenemos terminada la estructura del primer término de la igualdad. Ahora selecciona cada cuadradito y teclea el número correspondiente.
- Selecciona entonces el término medio de la igualdad y aplica el símbolo de División (fracción).
- Para que las operaciones que vamos a escribir en la fracción permanezcan en su sitio, hay que aplicar los Paréntesis de agrupamiento, del grupo de símbolos Paréntesis, a cada comodín de la fracción.
- Selecciona el comodín del numerador, transfórmalo en una suma y luego, cada sumando, en una multiplicación. Sustituye los comodines por los números.
- Transforma el denominador en una multiplicación y sustituye los comodines por los números.
- En el tercer término de la igualdad te basta con sustituir los comodines por sus respectivos valores.
Caso práctico 2. Subíndices y superíndices
La fórmula a construir es:
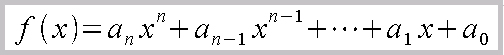
Pasos a seguir:
- Empieza creando la igualdad.
- Selecciona el segundo comodín de la igualdad (haz doble clic sobre el cuadradito) y pulsa cuatro veces el símbolo de la suma (+ de suma).
- Selecciona cada término de la suma menos el tercero y del grupo Formatos elige Subíndice derecha.
- Selecciona el tercer término y del grupo Otros aplica Puntos en el medio.
- Haz clic en el primer y segundo signo "+" sin seleccionarlo (el cursor de la ventana de comandos debe situarse delante del signo) y del grupo Formatos aplica Superíndice derecha.
- Haz clic en el último signo "+" y teclea una "x". Haz clic en el signo "=" y teclea "(x)" (siempre sin las comillas).
- La estructura ya está lista: selecciona cada cuadradito y teclea la expresión que debe reemplazarlo.
Caso práctico 3. Sumatorio
La fórmula a construir es:
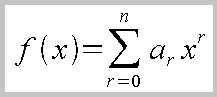
Pasos a seguir:
- Empieza creando la igualdad.
- Selecciona el segundo término de la igualdad y. del grupo Operadores. aplica primero el símbolo Suma y seguidamente el símbolo Límites superior e inferior.
- Pulsa sobre el último comodín sin seleccionarlo y del grupo Formatos aplica Subíndice derecha.
- Selecciona ahora el último comodín y aplica Superíndice derecha.
- La estructura ya está lista: selecciona cada comodín y teclea la expresión que deba reemplazarlo.
Caso práctico 4. Límites y paréntesis
La fórmula a construir es:
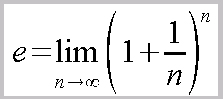
Pasos a seguir:
- Empieza creando la igualdad.
- Selecciona el primer término y pulsa la letra "e".
- Selecciona el segundo término y, del grupo Operadores, aplica primero el símbolo Límites y seguidamente el símbolo Límite inferior.
- Con el comodín pequeñito seleccionado, aplica el símbolo Tiende a del grupo Relaciones.
- Con el primer comodín pequeñito seleccionado, pulsa la letra "n" para poner n a la izquierda de la flecha.
- Selecciona el otro comodín pequeñito y aplica el símbolo Infinito del grupo Otros.
- Selecciona el comodín y aplica el símbolo Superíndice derecha del grupo Formatos.
- Con el comodín grande seleccionado, aplica el símbolo Paréntesis graduables del grupo Paréntesis y luego el símbolo + de suma del grupo Operadores unarios/binarios.
- Selecciona el segundo comodín grande y aplica el símbolo División (fracción).
- Por último, selecciona los comodines y teclea los valores correspondientes.