| a) Conocidos los catetos, calcular la hipotenusa.
|
|
|
|
b) Conocido un cateto y la hipotenusa, calcular el otro cateto.
En este caso debemos despejar el valor del cateto. a2 + b2 = c2
, de donde b2 = c2- a2 ,o bien a2 = c2
- b2 que son las expresiones que debemos aplicar.
1.-La hipotenusa de un triángulo rectángulo mide 5 cm. y uno
de los catetos, 3,2 cm. Calcula la medida del otro cateto.
b2 =
52 - 3,22=25- 10,24 =14,76
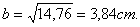
|
Haz los mismos cálculos para hipotenusa 5,3 cm. y un cateto 4,1 cm. Comprueba
el resultado en el gráfico.
** Los gráficos anteriores se han realizado de forma que los datos sean
números con una sola cifra decimal**.
2.- Conocidos los lados, saber si el triángulo es
obtusángulo, rectángulo o acutángulo.
Como hemos visto en un triángulo
rectángulo, el cuadrado de la hipotenusa es igual a la suma de los
cuadrados de los catetos.
|
En triángulos no
rectángulos no se habla de catetos e hipotenusa, pero si lado mayor,...
Observa la figura de la derecha, los tres segmentos
representan los lados de un triángulo (en caso de que exista).
Para
facilitar la construcción se representa el lado mayor (verde) en
horizontal, a la izquierda (azul) el mediano y a la derecha (rojo) el
menor.
Comprueba que si el cuadrado del lado mayor es mayor
que la suma de los cuadrados de los otros dos, el triángulo es
obtusángulo. Acutángulo si el cuadrado del lado mayor es menor que la
suma de los cuadrados de los otros dos.
El triángulo es rectángulo si el cuadrado del mayor es
igual a la suma del cuadrado de los otros dos. |
|
Si llamamos a, al lado mayor, b al mediano y c al pequeño. Se calcula a2
y se compara con b2 + c2 .
|
a2 > b2
+ c2 Obtusángulo |
a2 = b2
+ c2 Rectángulo |
a2 < b2
+ c2 Acutángulo |
3.- En muchas figuras geométricas podemos aplicar el
Teorema de Pitágoras
para calcular dimensiones desconocidas.
| El lado de un triángulo equilátero es 4 cm. ¿Cuánto vale la
altura?
Como ves en la figura puede aplicarse el Teorema de Pitágoras
construyendo un triángulo rectángulo por el punto medio de uno de los lados.
|
|
EJERCICIO
|
|
La figura representa un triángulo isósceles.
Mueve los vértices para que AB sea 4 cm. y AC=BC = 2,6 cm.
Calcula la altura aplicando el Teorema de Pitágoras.
Comprueba el
resultado con la regla (segmento) que aparece en la figura.
|
|