Los poliedros regulares estrellados
pueden crearse prolongando las caras de un convexo, mientras queden caras no paralelas
que aún no se encontrasen formando arista. Por esta razón no producen estrella
ni el tetraedro ni el hexaedro. Estas estrellas conservan el número de
caras, los planos de simetría y los ejes de rotación de los convexos
que los originan.
También pueden crearse estrellas
a partir de otros cuerpos como los poliedros semirregulares, por prolongación
de caras, o combinando poliedros de igual o diferente tipo.
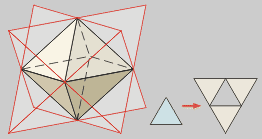
Octaedro
estrellado (Stella Octángula)
Prolongando las caras de un octaedro
se obtiene una única estrella, llamada por Kepler Stella Octángula.
También se construye combinando
dos tetraedros sobre una misma sección cuadrada.
|
|
|
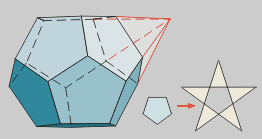
Dodecaedro estrellado
Prolongando las caras de un dodecaedro
(o bien las aristas, en este caso) se obtiene el Dodecaedro estrellado.
Las caras del convexo pasan de pentágonos
regulares convexos a estrellados.
|
|
|
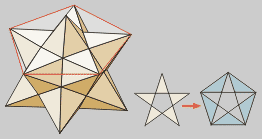
Dodecaedro grande
Prolongando las caras de un dodecaedro
estrellado, se obtiene la segunda estrella, llamada Dodecaedro Grande.
La silueta exterior de las caras recupera
la forma de pentágono regular convexo.
|
|
|
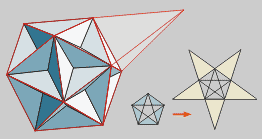
Dodecaedro grande estrellado
Prolongando las caras de un dodecaedro
grande, se obtiene la tercera y última estrella, llamada Dodecaedro
Grande estrellado.
La forma de las caras vuelve a ser un
pentágono regular estrellado.
|
|
|
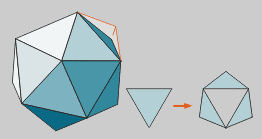
Icosaedro estrellado
Prolongando las caras de un icosaedro
se obtiene la primera estrella, el icosaedro estrellado.
Las caras del convexo pasan de triángulos
equiláteros a hexágonos irregulares definidos por
triángulos con los lados en razón áurea, como
en el dodecaedro grande.
|
|
|
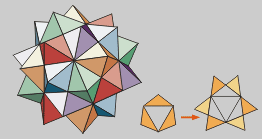
Icosaedro segunda estrella
Prolongando las caras de un icosaedro
estrellado se obtiene una segunda estrella más irregular,
ya que cada cara adopta la forma de dos triángulos equiláteros
superpuestos.
También puede construirse
combinando cinco octaedros regulares.
|
|
|
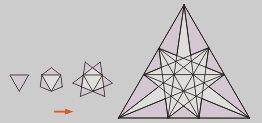
Icosaedro grande
En la última pulsación,
cuando cada una de las caras del icosaedro convexo formó arista con
todas las demás, se recupera la forma de triángulo
equilátero, por lo que se denomina Icosaedro Grande.
La zona visible de cada cara se determina
fácilmente sabiendo que los puntos de incidencia con las otras
están en la sección áurea de los lados exteriores
del triángulo.
|
|
|
Formas compuestas
estrelladas
Del mismo modo que la Estella
octángula es la combinación de dos tetraedros, otros
dos sólidos interesantes nacen de combinar poliedros regulares duales
o conjugados: el hexaedro con el octaedro, y el dodecaedro con el icosaedro.
Cuando inscribimos uno en el otro, hacemos que la esfera circunscrita del interior
coincida con la inscrita del exterior, pero en este caso lo que hacemos es
igualar las esferas medias de ambos, y así las aristas se cortan perpendicularmente
en los puntos medios.
La combinación de hexaedro
con octaedro genera como sólido común un cuboctaedro, y como
sólido envolvente el dual de este, llamado Dodecaedro rómbico
y clasificado en el grupo de sólidos de Catalán.
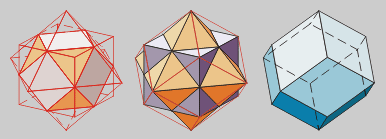
La combinación de dodecaedro
con icosaedro genera como sólido común un triakontágono,
y como sólido envolvente el dual de este, llamado Triakontaedro rómbico,
también sólido de Catalán.

Dodecaedro rómbico
estrellado
Las caras del Dodecaedro rómbico,
como las del triacontaedro, son rombos con las diagonales en proporción
1 a raíz de 2. También se forma adosando a un cubo
pirámides como las que forman sus caras con el centro.
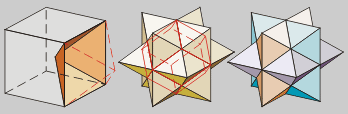
Su estrella, que es como tres octaedros achatados,
tiene la particularidad de ser la única con la que se puede teselar
el espacio.
|
|
|
|

