Están
formados por dos o tres tipos de polígonos regulares.
No tienen esfera
inscrita, pero conservan la media y la circunscrita.
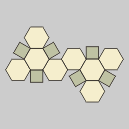
Pueden construirse a partir de los regulares mediante algún tipo
de modificación, como el Truncamiento o
la ablación.
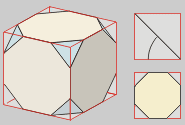
El truncamiento de un vértice supone seccionar el poliedro con un plano perpendicular
al radio correspondiente. El truncamiento de una arista se hace también
con un plano perpendicular al radio de la circunferencia media que une el centro
del poliedro con el punto medio de la arista.
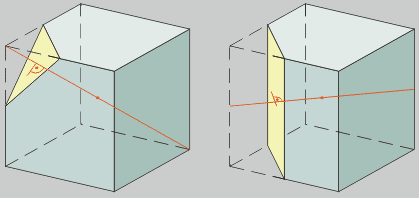
Los poliedros semirregulares
obtenidos por truncamiento conservan los ejes y planos de simetría
de los regulares.
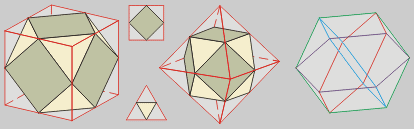
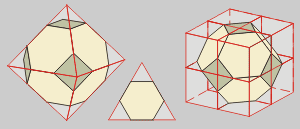
Podemos comenzar truncando
los vértices de los cinco poliedros regulares con planos que pasan
por los puntos medios de las aristas. Del tetraedro no resulta un tipo nuevo
de sólido, sinó un octaedro:
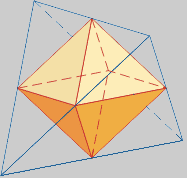
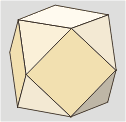
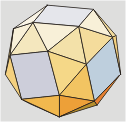
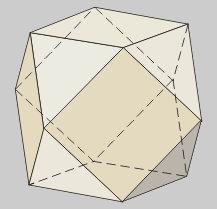
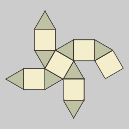
Cuboctaedro
|
|
Caras:
Aristas:
Vértices:
Radio:
Superficie:
Volumen: |
14 (6 cuadrados y
8 triángulos)
24
12 (3/4/3/4)
1 a
9.4641
a2
2.357
a3 |
|
Es el poliedro
resultante de truncar hasta los puntos medios de las aristas
los vértices de un hexaedro o de un octaedro.
Puede definirse fácilmente
con cuatro hexágonos regulares. |
|
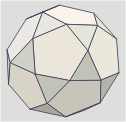
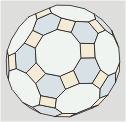
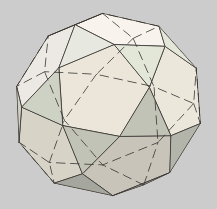
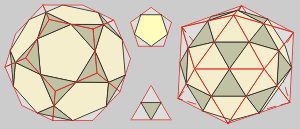
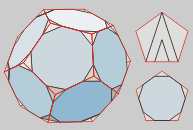
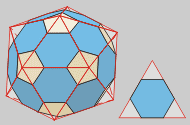
Triakontágono
|
|
Caras:
Aristas:
Vértices:
Radio:
Superficie:
Volumen: |
32 (12 pentágonos y 20 triángulos)
60
30 (3/5/3/5)
1,618
a
29.306
a2
13.835
a3 |
|
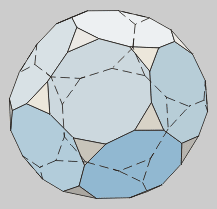
Llamado también
Icosidodecaedro.
Es el resultado de truncar
hasta los puntos medios de las aristas los vértices
de un dodecaedro o de un icosaedro. |
|
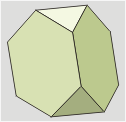
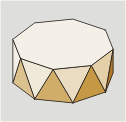
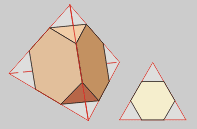
Tetraedro
truncado
|
|
Caras:
Aristas:
Vértices:
Radio:
Superficie:
Volumen: |
8 (4 hexágonos y 4 triángulos)
18
12 (3/6/6)
1,1726
a
12.1243
a2
2.71
a3 |
|
Llamado también
Troncotetraedro.
Es el resultado de truncar
hasta un tercio de la arista los vértices de un tetraedro. |
|
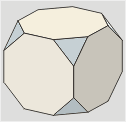
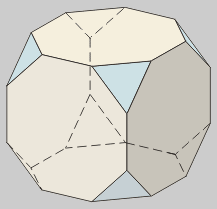
Hexaedro
truncado
|
|
Caras:
Aristas:
Vértices:
Radio:
Superficie:
Volumen: |
14 (8 triángulos y 6 octógonos)
36
24 (3/8/8)
1.7788
a
32.434
a2
13.599
a3 |
|
Llamado también
Troncohexaedro.
Es el resultado de truncar
los vértices de un hexaedro hasta 0,2929 de la arista. 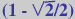 |
|
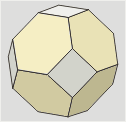
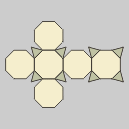
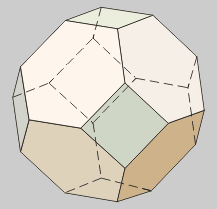
Octaedro
truncado
|
|
Caras:
Aristas:
Vértices:
Radio:
Superficie:
Volumen: |
14 (8 hexágonos y 6 cuadrados)
36
24 (4/6/6)
1.581
a
26.784
a2
11.3137
a3 |
|
Llamado también
Troncooctaedro y Poliedro de Lord Kelvin.
Es el resultado de
truncar los vértices de un octaedro hasta un tercio
de la arista. Es el único sólido semirregular con el que se
puede teselar el espacio. |
|
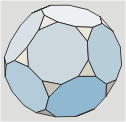
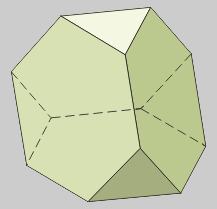
Dodecaedro
truncado
|
|
Caras:
Aristas:
Vértices:
Radio:
Superficie:
Volumen: |
32 (20 triángulos y 12 decágonos)
90
60 (3/10/10)
2.969
a
100.99
a2
85.039
a3 |
|
Llamado también
Troncododecaedro.
Es el resultado de truncar
los vértices de un dodecaedro hasta 0,276 de la arista.
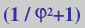 |
|
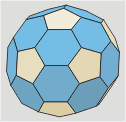
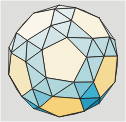
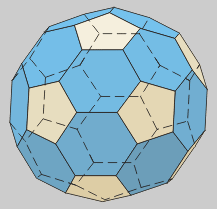
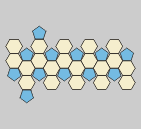
Icosaedro
truncado
|
|
Caras:
Aristas:
Vértices:
Radio:
Superficie:
Volumen: |
32 (20 hexágonos y 12 pentágonos)
90
60 (5/6/6)
2.478
a
72.607
a2
55.287
a3 |
|
Llamado también
Troncoicosaedro.
Es el resultado de truncar
los vértices de un icosaedro hasta un tercio de la arista.
|
|
|