Os poliedros regulares estrelados
poden crearse prolongando as caras dun convexo, mentras queden caras non paralelas
que aínda non formasen arista. Por esta razón non producen estrela
nin o tetraedro nin o hexaedro. Estas estrelas conservan o número de
caras, os planos de simetría e os eixos de rotación dos convexos
que os orixinan.
Tamén poden crearse estrelas
a partir doutros corpos como os poliedros semirregulares, por prolongación
de caras, ou combinando poliedros de igual ou diferente tipo.
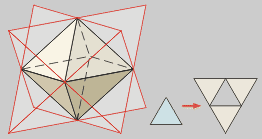
Octaedro
estrelado (Stella Octángula)
Prolongando as caras dun octaedro
obtense unha única estrela, chamada por Kepler Stella Octángula.
Tamén se construe combinando
dous tetraedros sobre unha mesma sección cadrada.
|
|
|
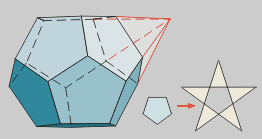
Dodecaedro estrelado
Prolongando as caras dun dodecaedro
(ou ben as aristas, neste caso) obtense o Dodecaedro estrelado.
As caras do convexo pasan de pentágonos
regulares convexos a estrelados.
|
|
|
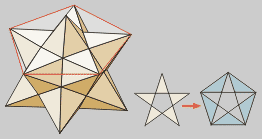
Dodecaedro grande
Prolongando as caras dun dodecaedro
estrelado, obtense a segunda estrela, chamada Dodecaedro Grande.
A silueta exterior das caras recupera
a forma de pentágono regular convexo.
|
|
|
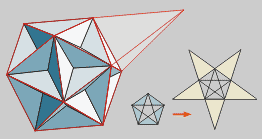
Dodecaedro grande estrelado
Prolongando as caras dun dodecaedro
grande, obtense a terceira e última estrela, chamada Dodecaedro
Grande estrelado.
A forma das caras volve ser un
pentágono regular estrelado.
|
|
|
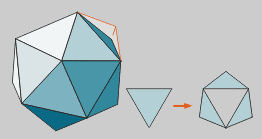
Icosaedro estrelado
Prolongando as caras dun icosaedro
obtense a primeira estrela, o icosaedro estrelado.
As caras do convexo pasan de triángulos
equiláteros a hexágonos irregulares definidos por
triángulos cos lados en razón áurea, como
no dodecaedro grande.
|
|
|
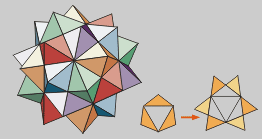
Icosaedro segunda estrela
Prolongando as caras dun icosaedro
estrelado obtense unha segunda estrela máis irregular,
xa que cada cara adopta a forma de dous triángulos equiláteros
superpostos.
Tamén pode construirse
combinando cinco octaedros regulares.
|
|
|
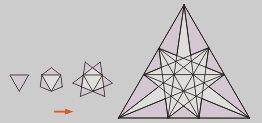
Icosaedro grande
Na última pulsación,
cando cada unha das caras do icosaedro convexo fixo arista con
todas as demáis, recupérase a forma de triángulo
equilátero, polo que se denomina Icosaedro Grande.
A zona visible de cada cara determínase
fácilmente sabendo que os puntos de incidencia coas outras
están na sección áurea dos lados exteriores
do triángulo.
|
|
|
Formas compostas
estreladas
Do mesmo xeito que a Estella
octángula é a combinación de dous tetraedros, outros
dous sólidos interesantes nacen de combinar poliedros regulares duais
ou conxugados: o hexaedro co octaedro, e o dodecaedro co icosaedro.
Cando inscribimos un no outro, facemos que a esfera circunscrita do interior
coincida coa inscrita do exterior, pero neste caso o que facemos é
igualar as esferas medias de ambos os dous, e así as aristas córtanse perpendicularmente
nos puntos medios.
A combinación de hexaedro
con octaedro xera como sólido común un cuboctaedro, e como
sólido envolvente o dual deste, chamado Dodecaedro rómbico
e clasificado no grupo de sólidos de Catalán.
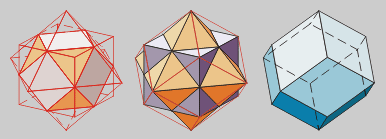
A combinación de dodecaedro
con icosaedro xera como sólido común un triakontágono,
e como sólido envolvente o dual deste, chamado Triakontaedro rómbico,
tamén sólido de Catalán.

Dodecaedro rómbico
estrelado
As caras do Dodecaedro rómbico,
como as do triacontaedro, son rombos coas diagonais en proporción
1 a raíz de 2. Tamén se forma achegando a un cubo
pirámides como as que forman as súas caras co centro.
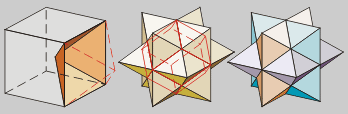
A súa estrela, que é como tres octaedros achatados,
ten a particularidade de ser a única coa que se pode teselar
o espacio.
|
|
|
|