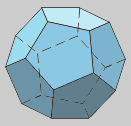
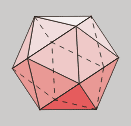
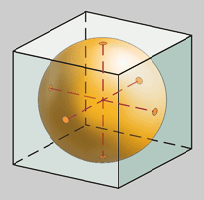
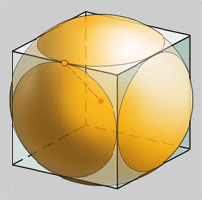
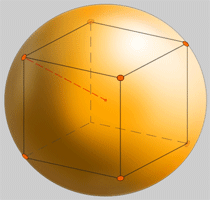
Dado que todas as caras dun poliedro
regular equidistan do centro, existe unha esfera
inscrita tanxente a todas elas. O seu diámetro é
a distancia entre caras opostas.
A esfera media pasa polos puntos medios
de todas as aristas. O seu diámetro é a distancia
entre aristas opostas.
A esfera circunscrita pasa por todos
os vértices. O seu diámetro é a distancia entre
vértices opostos. Cando se fala de raio
do poliedro, refírese ao raio desta esfera.
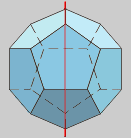
Estes poliedros teñen eixos
de rotación e planos de simetría, característicos
da súa regularidade. Todos pasan polo centro e por puntos
significativos como vértices, puntos medios de aristas
e centros de caras.
|
|
Na rotación dun
poliedro arredor dun eixo danse momentos en que a posición
é idéntica á inicial, a intervalos
divisores de 360º.
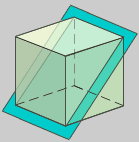
Un plano de simetría
divide o poliedro en dúas
partes que son imaxe especular unha da outra.
Cada punto dun lado do plano é replicado por outro
no lado contrario, á mesma distancia do plano.
|
|
*
Dualidade ou
polaridade
É a relación entre
un poliedro dado e o resultante de situar un vértice no
centro de cada cara.
Serán duais, polares ou conxugados os poliedros regulares
que teñan o mesmo sistema de eixos de simetría.
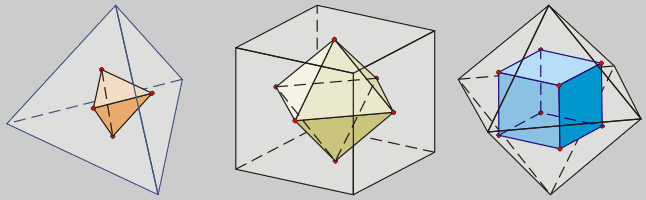
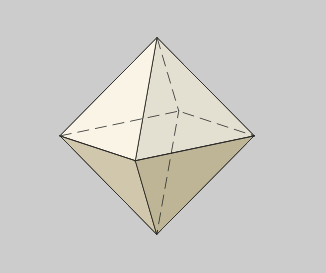
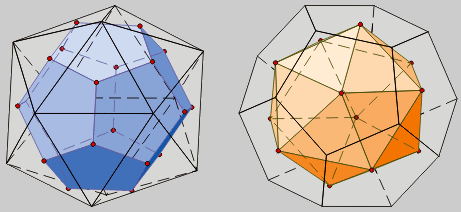
O tetraedro é
autopolar, o seu dual é outro tetraedro.
O hexaedro e o octaedro son duais un do outro, como tamén
o dodecaedro e o icosaedro.
*
Desenvolvementos
planos
|
|
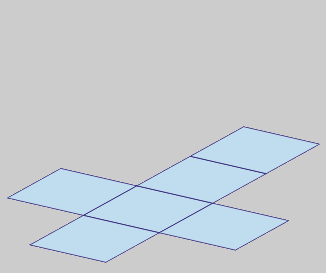
Podemos construir calquera
poliedro regular a partir dunha figura plana na que están
despregadas todas as caras. Esta
figura é o desenvolvemento plano
(podes pasar o rato sobre
a figura da dereita)
Teóricamente o desenvolvemento
obtense a partir da figura facendo abatementos das súas
caras que xiran sobre as aristas.
Na sección Desenvolvementos
ofrecemos unha colección
en pdf listos para imprimir e construir as figuras |
*
Estrelas
Prolongando os lados
dun polígono regular de 5 lados ou máis, aparecen
polígonos estrelados.
Do mesmo xeito, prolongando as caras dun poliedro regular podemos
crear poliedros estrelados.
A estrela aparece cando
caras que antes non formaban aristas se atopan. O tetraedro non
produce estrela porque cada cara xa forma arista con todas as demáis.
O hexaedro tampouco porque cada cara forma arista con todas as demáis
menos unha, pero ésta é paralela así que non
intersectan ainda que se prolonguen.
*
Seccións
As seccións son as figuras
planas que se producen cando un plano intersecta un sólido.
Dependendo da orientación do plano respecto das liñas
principais do poliedro, as seccións resultantes poden ser
formas xeométricas características.
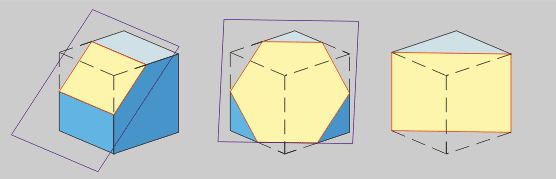
En todos os poliedros
regulares é posible facer unha sección na que se recollen
as principais magnitudes da figura. Chámase Sección
principal.
*
Magnitudes e cálculos
As medidas liñais e angulares
dos poliedros poden calcularse coa axuda de diferentes recursos.
Para o cálculo gráfico son de moita axuda as seccións
principais, e para o numérico a aplicación de recursos
básicos como o teorema de Pitágoras ou a trigonometría.
A Superficie
do poliedro é igual á suma das áreas das caras.
O Volume
do poliedro é igual ao dunha pirámide que ten como
base unha das caras e como altura a apotema do poliedro, multiplicado
polo número de caras. (volume que é igual a un tercio
do prisma de igual base e altura).
A Apotema
do poliedro é o raio da circunferencia inscrita. É
o cateto dun triángulo rectángulo no que a hipotenusa
é o raio do poliedro e o outro cateto o raio do polígono
que forma a cara.