|
|
|
|
|
||||||||
|
|
|
|
 |
|
|
|
|||||
|
|
|
||||||||||
|
|
|
|
|||||||||
 |
|
||||||||||
 |
|
||||||||||
| |
|
||||||||||
|
|
|
|
|||||||||
|
|
|
|
|||||||||
|
|
|
||||||||||
|
|
|
||||||||||
| |
 |
|
|
||||||||
|
|
|
|
|
||||||||
| |
|
|
|
|
|
|
|
|
|
|
|
* Superficie
|
* Volume
|
* Eixos de simetría
16 eixos. 6 pasan por dous vértices e 10 polos centros de dúas caras* Poliedro dual
O dual do Icosaedro é o Dodecaedro* Desenvolvemento
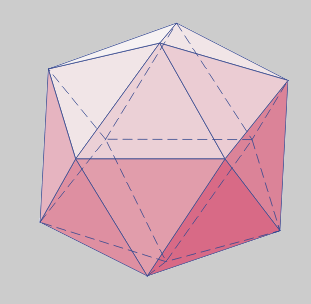
* Inscrición nos outros poliedros regulares
No tetraedro catro caras están centradas coas do poliedro circunscrito. As aristas do icosaedro, prolongadas, cortan os vértices e as seccións áureas das aristas do tetraedro.
Nas caras do hexaedro sitúanse seis aristas centradas que son sección áurea das do cubo.
No Octaedro cada vértice sitúase na sección áurea dunha arista.
No Dodecaedro cada vértice está no centro dunha cara. Os poliedros son duais.
* Estrelas
Icosaedro Estrelado
(prolongación das caras)
Icosaedro Grande
(prolongación das
caras do estrelado)
* Sección principal
a = arista.
hc = altura de cara.
dc = distancia entre caras opostas.
da = distancia entre aristas opostas.
dv = distancia entre vértices opostos.
* Relacións áureas
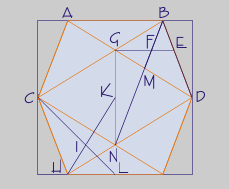
Posicións en sistema diédrico sobre un vértice:
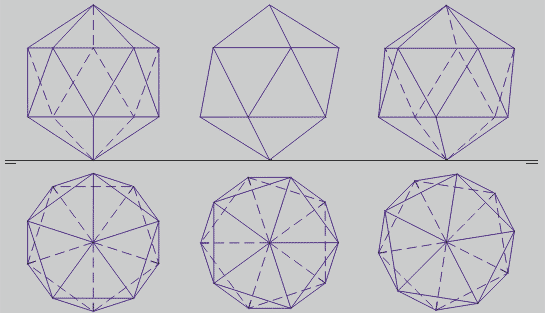
Construción: Pártese dun pentágono regular como base. Trázase a circunferencia circunscrita e prolongando os raios sitúase a base superior. Trázanse o decágono que será o contorno da vista, unha perpendicular ao raio AO dende O e unha perpendicular ao segmento AD dende D. Con centro en A, un arco de raio igual ao lado AC dará nas perpendiculares as alturas h e H para a segunda proxección, que gardan a proporción áurea. A altura total dv é H+2h.
Posicións en sistema diédrico sobre unha arista:
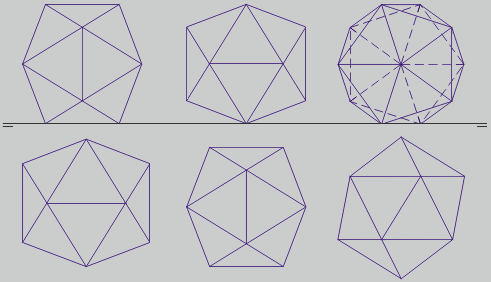
A primeira proxección é semellante a unha sección principal. Na segunda, a altura total é da (distancia entre aristas opostas), a súa sección áurea a (arista), a metade da sección áurea de a (h), e a suma de a + h (H):
Posicións en sistema diédrico sobre unha cara:
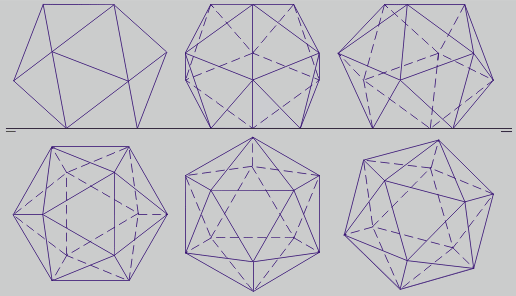
A primeira proxección constrúese a partir dun triángulo equilátero base, a súa circunferencia circunscrita e outro triángulo xirado 180º. Prolongando os raios dos 6 vértices e xuntando un pentágono a un dos lados localízanse fácilmente os 6 vértices exteriores en forma de hexágono regular. Os raios dos triángulos e do hexágono están en proporción áurea.
Para calcular as alturas, trázanse perpendiculares nos extremos do diámetro CB, mediatriz do lado no que xuntámos o pentágono, e dende o punto medio deste lado (A), as alturas do triángulo e do pentágono dan as da segunda proxección, H e h. h é sección áurea de H, e H sección áurea da altura total dc (distancia entre caras opostas):