|
|
|
|
|
||||||||
|
|
|
|
 |
|
|
|
|||||
|
|
|
||||||||||
|
|
|
|
|||||||||
 |
|
||||||||||
 |
|
||||||||||
| |
|
||||||||||
|
|
|
|
|||||||||
|
|
|
|
|||||||||
|
|
|
||||||||||
|
|
|
||||||||||
| |
 |
|
|
||||||||
|
|
|
|
|
||||||||
| |
|
|
|
|
|
|
|
|
|
|
|
* Superficie
|
* Volumen
|
* Ejes de simetría
16 ejes. 6 pasan por dos vértices y 10 por los centros de dos caras* Poliedro dual
El dual del Icosaedro es el Dodecaedro* Desenvolvimiento
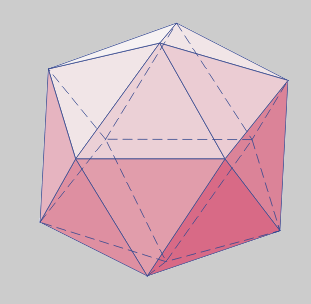
* Inscripción en los otros poliedros regulares
En el Tetraedro cuatro caras están centradas con las del poliedro circunscrito. Las aristas del Icosaedro, prolongadas, cortan los vértices y las secciones áureas de las aristas del Tetraedro.
En las caras del Hexaedro se sitúan seis aristas centradas que son secciones áureas de las del cubo.
En el Octaedro cada vértice se sitúa en la sección áurea de una arista.
En el Dodecaedro cada vértice está en el centro de una cara. Los poliedros son duales.
* Estrellas
Icosaedro Estrellado
(prolongación de las caras)
Icosaedro Grande
(prolongación de las
caras del estrellado)
* Sección principal
a = arista.
hc = altura de cara.
dc = distancia entre caras opuestas.
da = distancia entre aristas opuestas.
dv = distancia entre vértices opuestos.
* Relaciones áureas
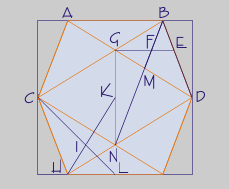
Posiciones en sistema diédrico sobre un vértice:
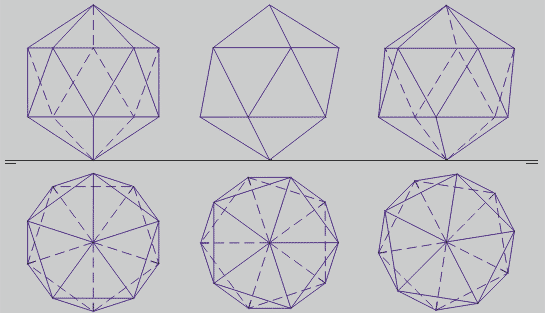
Construción: Se parte de un pentágono regular como base. Se traza la circunferencia circunscrita y prolongando los radios se sitúa la base superior. Se traza el decágono que será el contorno de la vista, una perpendicular al radio AO desde O y una perpendicular al segmento AD desde D. Con centro en A, un arco de radio igual al lado AC dará en las perpendiculares las alturas h y H para la segunda proyección, que guardan la proporción áurea. La altura total dv es igual a H+2h.
Posiciones en sistema diédrico sobre una arista:
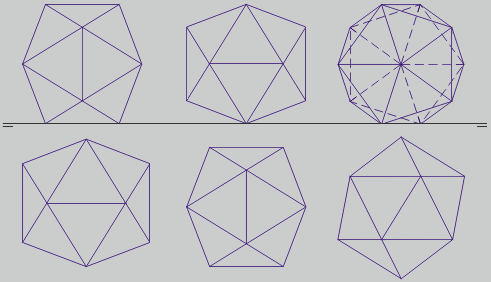
La primera proyección es semejante a una sección principal. En la segunda, la altura total es da (distancia entre aristas opuestas), su sección áurea a (arista), la mitad de la sección áurea de a (h), y la suma de a + h (H):
Posiciones en sistema diédrico sobre una cara:
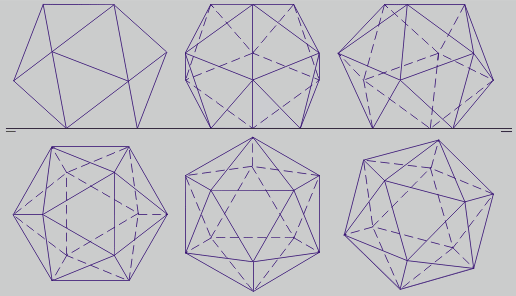
La primera proyección se construye a partir de un triángulo equilátero base, su circunferencia circunscrita y otro triángulo girado 180º. Prolongando los radios de los 6 vértices y adosando un pentágono a uno de los lados se localízan fácilmente los 6 vértices exteriores en forma de hexágono regular. Los radios de los triángulos y del hexágono están en proporción áurea.
Para calcular las alturas, se trazan perpendiculares en los extremos del diámetro CB, mediatriz del lado en el que hemos adosado el pentágono, y desde el punto medio de este lado (A), las alturas del triángulo y del pentágono dan las de la segunda proyección, H y h. h es sección áurea de H, y H sección áurea de la altura total dc (distancia entre caras opuestas):