Rombicuboctaedro
pequeno
|
|
Caras:
Aristas:
Vértices:
Raio:
Superficie:
Volume: |
26
(18 cadrados e
8 triángulos)
48
24
(3/4/4/4)
1.3989
a
21.464
a2
8.714
a3 |
|
Comúnmente
se di que este poliedro resulta de truncar até a metade
das aristas un cuboctaedro, pero así resultan rectángulos, non
cadrados.
A maneira correcta é truncar os
vértices dun cadrado inicial até o 58,58% 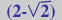 |
|
Trúncanse logo as aristas pequenas do
sólido resultante até o punto medio das aristas
das caras cadradas. |
|
Pseudo-Rombicuboctaedro
|
|
Caras:
Aristas:
Vértices:
Raio:
Superficie:
Volume: |
26
(18 cadrados e
8 triángulos)
48
24
(3/4/4/4)
1.3989
a
21.464
a2
8.714
a3 |
|
Deriva do Rombicuboctaedro
pequeno, ao que se pode rotar 45º un casquete (cúpola)
de 5 cadrados e 4 triángulos.
Alteracións semellantes
poden facerse co cuboctaedro ou co triakontágono, pero
pérdese a igualdade nos ángulos sólidos.
O pseudo-Rombicuboctaedro
perde os planos de simetría que pasan polo eixo de
xiro, pero non a igualdade dos ángulos. |
|
Rombicuboctaedro
grande
|
|
Caras:
Aristas:
Vértices:
Raio:
Superficie:
Volume: |
26
(12 cadrados, 8 hexágonos e 6 octógonos)
48
24
(4/6/8)
2.3176
a
61.755
a2
41.798
a3 |
|
Truncamos os vértices
dun cadrado inicial até o 58,58% 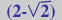 como
no rombicuboctaedro pequeno, e logo
truncamos as aristas pequenas do sólido até
0,2929 da arista das caras cadradas como
no rombicuboctaedro pequeno, e logo
truncamos as aristas pequenas do sólido até
0,2929 da arista das caras cadradas 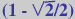 |
|
Rombicosidodecaedro
pequeno
|
|
Caras:
Aristas:
Vértices:
Raio:
Superficie:
Volume: |
62
(20 triángulos, 30 cadrados e 12 hexágonos)
120
60
(3/4/5/4)
2.233
a
59.3
a2
41.615
a3 |
|
Este poliedro
NON resulta de truncar un triakontágono até
o punto medio das aristas. O truncamento dos vértices
do dodecaedro inicial debe chegar aos 2/3 da arista.
(sería de esperar que fose até a sección
áurea, pero son 2/3).
Trúncanse logo as aristas
pequenas do sólido resultante até o punto medio
das aristas das caras pentagonais. |
|
Rombicosidodecaedro
grande
|
|
Caras:
Aristas:
Vértices:
Raio:
Superficie:
Volume: |
62
(30 cadrados, 20 hexágonos e 12 decágonos)
180
120
(4/6/10)
3,8 a
174.29
a2
206.8
a3 |
|
Truncamos os vértices
dun dodecaedro inicial até a sección áurea
das aristas (61,8%).
No sólido resultante,
truncamos as aristas pequenas até o 27,6% da arista das
caras pentagonais, que se converten en decágonos.
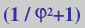 |
|
Hexaedro
achatado
|
|
Caras:
Aristas:
Vértices:
Raio:
Superficie:
Volume: |
38
(32 triángulos e 6 cadrados)
60
24
(3/3/3/3/4)
1.3437
a
19.856
a2
7.889
a3 |
|
Non se obtén
por truncamento, ainda que as caras cadradas poden inscribirse
nas dun hexaedro, xiradas todas no mesmo sentido, polo que
existen dúas formas: dextra e leva.
Non ten planos de simetría,
pero sí eixos. |
|
Dodecaedro
achatado
|
|
Caras:
Aristas:
Vértices:
Raio:
Superficie:
Volume: |
92
(80 triángulos e 12 pentágonos)
150
60
(3/3/3/3/5)
2.1558
a
55.2867
a2
37.6166
a3 |
|
Non se obtén por truncamento.
As caras pentagonais inscríbense xiradas nun dodecaedro, polo
que existen dúas formas: dextra e leva.
As alturas e os lados prolongados
cortan as aristas do dodecaedro segundo a sección áurea.
Non ten planos
de simetría, pero sí eixos. |
|
Prismas
e Antiprismas
Completan as
posibilidades de crear poliedros con dous tipos de polígono
regular.
Os prismas xéranse interpoñendo entre dous polígonos
regulares iguais tantos cadrados como lados ten cada un. |
|
| Os antiprismas
xéranse interpoñendo entre dous polígonos
regulares iguais e rotados a metade do seu ángulo central,
tantos triángulos equiláteros como lados teñen
entre os dous. |
|
|