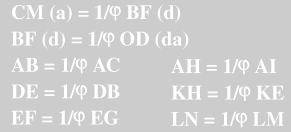|
|
|
|
|
||||||||
|
|
|
|
 |
|
|
|
|||||
|
|
|
||||||||||
|
|
|
|
|||||||||
 |
|
||||||||||
 |
|
||||||||||
|
|
|
||||||||||
|
|
|
|
|||||||||
|
|
|
|
|||||||||
|
|
|
||||||||||
|
|
|
||||||||||
| |
 |
|
|
||||||||
|
|
|
|
|
||||||||
| |
|
|
|
|
|
|
|
|
|
|
|
* Superficie
|
* Volumen
|
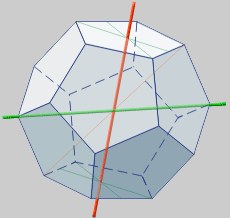
* Ejes de simetría
16 ejes. 10 pasan por dos vértices y 6 por los centros de dos caras* Poliedro dual
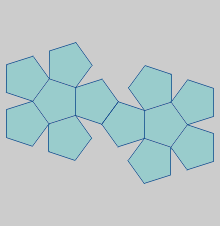
El dual del Dodecaedro es el Icosaedro* Desenvolvimiento
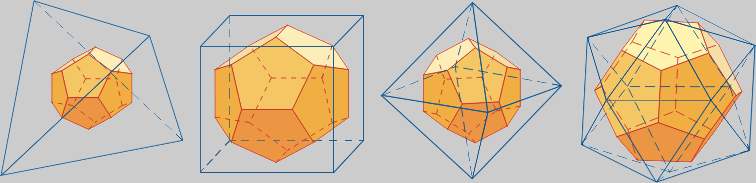
* Inscripción en los otros poliedros regulares
En los tres primeros no hay una inscripción completa. En el Tetraedro cuatro vértices están en los centros de las caras.
En las caras del hexaedro se sitúan seis aristas centradas con una proporción de 1 arespecto a las del cubo. Los ocho vértices no inscritos forman otro cubo de arista la sección áurea del exterior.
En el Octaedro ocho vértices están en los centros de las caras, que son los del cubo inscrito dual del octaedro.
En el Icosaedro cada vértice está en el centro de una cara. Los poliedros son duales.
* Estrellas
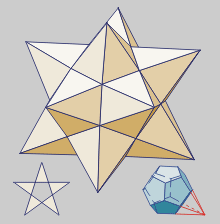
Dodecaedro Estrellado
(prolongación de las
caras o aristas del
convexo)
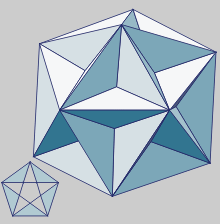
Dodecaedro Grande
(prolongación de las
caras del estrellado)
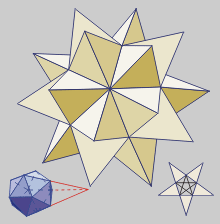
Dodecaedro Grande
Estrellado
(prolongación de las caras
del Grande, o aristas del
icosaedro circunscrito)
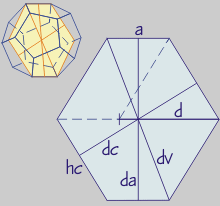
* Sección principal
a = arista. d = diagonal de cara.
hc = altura de cara.
dc = distancia entre caras opuestas.
da = distancia entre aristas opuestas.
dv = distáncia entre vértices opuestos.
* Relaciones áureas
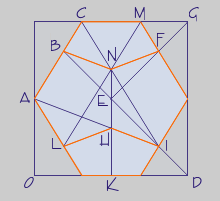
Posiciones en sistema diédrico sobre una cara:
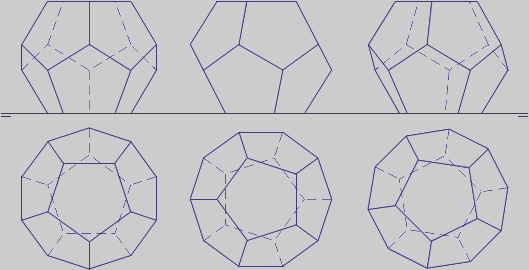
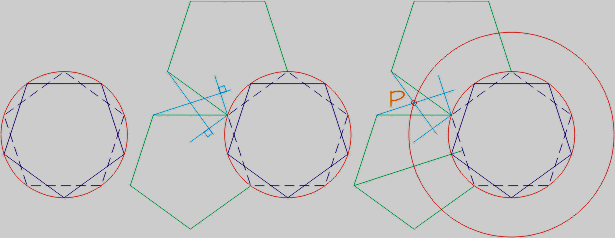
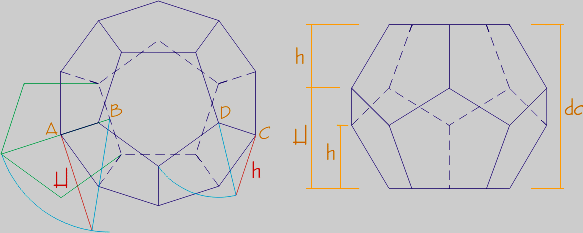
Construción: Se parte de un pentágono regular como base. Se traza la circunferencia circunscrita y la base superior. Se adosan a la base otros dos pentágonos como caras abatidas. Desde los dos vértices que se juntan en el poliedro se trazan perpendiculares a las charnelas, cruzándose en el punto P, por el que se traza otra circunferencia concéntrica:
Otra manera de trazarla es sabiendo que los radios de las dos circunferencias están en razón áurea.
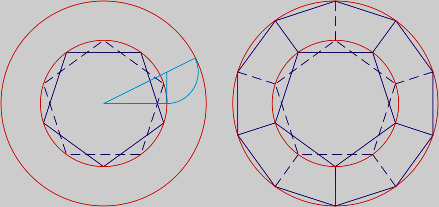
En la segunda circunferencia se sitúan fácilmente los vértices que faltan:
Para la segunda proyección, las alturas se calculan por abatimiento:
Por A se traza una perpendicular a AB. Desde B se lleva la verdadera magnitud de la altura del pentágono, resultando la altura H.
Por C se traza una perpendicular a CD. Desde D se lleva la verdadera magnitud de la arista, resultando la altura h.
h es sección áurea de H, y H sección áurea de la distancia entre caras dc, que también es la suma de H y h:
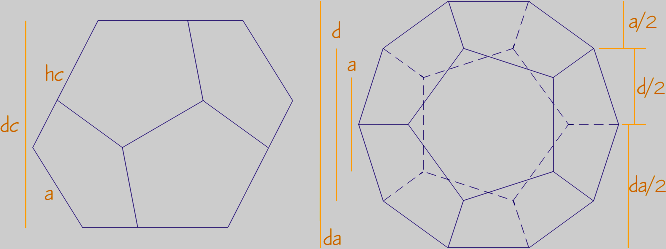
Posiciones en sistema diédrico sobre una arista:
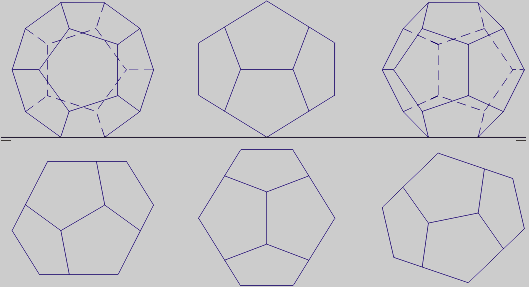
La primera proyección es similar a una sección principal. En la segunda, las alturas a utilizar son la arista (a), la diagonal de cara (d) y la distancia entre aristas opuestas (dc). Cada una es sección áurea de la siguiente:
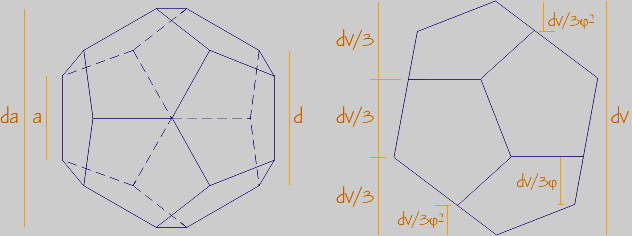
Posiciones en sistema diédrico sobre un vértice:
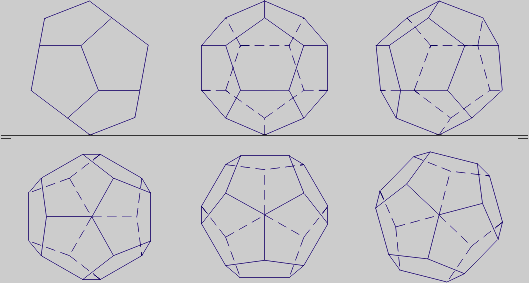
En la primera proyección aparecen en verdadera magnitud las medidas a, d, dc. En la segunda, la altura es la distancia entre vértices opuestos (dv). Se divide en tres tramos iguales, y la sección áurea de los tercios da las alturas restantes: