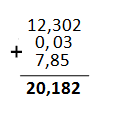- Números decimales
- Guía para el profesorado
DIRECCIÓN: Narcís Vives
COLABORADORES:
- PRODUCCIÓN EJECUTIVA: Antonio Cara
- DIRECCIÓN CONTENIDOS: Mª Cristina Pérez y Magdalena Garzón
- DIRECCIÓN TÉCNICA: Maite Vílchez
- COORDINACIÓN ÁREA MATEMÁTICAS: José Orenga
- AUTORÍA: Josep Pons y José Orenga
- CORRECCIÓN ESTILO VERSIÓN CASTELLANA: Anna Betriu y Joan Martín
- ADAPTACIÓN EUSKERA: Bakun itzulpen eta argitalpen zerbitzuak, s.l.
- MAQUETACIÓN: Maite Vílchez y Miquel Gordillo
Presentación
Los números decimales
| Seguramente, a vuestro alrededor habéis visto unos números que llevan una coma separando sus cifras. Estos números se llaman números decimales. ¿Estáis listos para investigar su significado? ¡Manos a la obra! |
|
|
Explora, crea, publica y comparte
Actividad 1
¿Qué son los números decimales?
Vamos a ver la relación entre los números decimales y las fracciones decimales. Aprenderemos como se leen los números decimales y también como se escriben.
En ocasiones sucede que al querer repartir una cantidad entre varios hermanos o un grupo de amigos, no podemos dividirla en partes exactas. De estas divisiones surgen los números decimales.
En efecto, observad la imagen y pensad cómo podremos repartir 9 galletas entre cuatro amigos. Al dividir 9 entre 4, hasta obtener resto 0, obtenemos el número 2,25. Es un número decimal que está entre el 2 y el 3, más cerca del 2.
Si pensáis en situaciones de la vida real veréis que la mayoría de números son decimales. Pensad, por ejemplo, en lo que se paga por cada litro de combustible: 1,064€; o el precio de un kilo de peras: 1,79€; o vuestra estatura, ¿es un valor exacto? ¿Recordáis cuánto costó la entrada de cine la última vez? Pensad en estos números y en cómo se leen.
Observad en la siguiente presentación otras situaciones en las que aparecen los números decimales en nuestra vida cotidiana: Números decimales.
Los números decimales pueden leerse indicando el valor de sus cifras o leyendo las dos partes en que se separan, la parte entera a la izquierda de la coma, y la parte decimal a la derecha:
Parte entera |
Parte decimal |
|||||
| decenas | unidades | décimas | centésimas | milésimas | ||
| 54,315 | 5 |
4 |
, |
3 |
1 |
5 |
Así, el número 54,315 se puede leer:
Cincuenta y cuatro unidades trescientas quince milésimas,o bien,
Cincuenta y cuatro coma trescientos quince.Observad que los ceros al final de un número decimal no varían el valor de ese número. Podéis comprobar que:
45,2 = 45,20 = 45,200
Un número decimal exacto, es decir, con una cantidad limitada de cifras decimales, siempre podrá representarse mediante una fracción decimal. Así, tenemos que:
2,25 = 225/100
Podemos observar que el numerador se ha formado tomando el número sin la coma y el denominador tomando un “1” seguido de tantos ceros como cifras decimales.
Recordad:
1/10 = 1:10 = 0,1 (una décima) | 4/10 = 4:10 = 0,4 (cuatro décimas) |
1/100 = 1:100 = 0,01 (una centésima) | 4/100 = 4:100 = 0,04 (cuatro centésimas) |
1/1000 = 1:1000 = 0,001 (una milésima) | 4/1000 = 4:1000 = 0,004 (cuatro milésimas) |
ACTIVIDADES
Resolved las siguientes actividades y escribid vuestras respuestas en un archivo de texto:
| a) 4,05 | b) 4,5 | c) 5,4 | d) 6,102 | e) 25,19 | f) 23,168 |
- 27 unidades 2 centésimas.
- 7 unidades 6 décimas 5 milésimas.
- 12 unidades 10 milésimas.
- 401 unidades 1 milésima.
- 8 centenas 1 décima 2 centésimas.
- 2 décimas 3 milésimas.
Haced clic en la imagen para utilizar la calculadora:
Y si tenéis dudas consultad este manual.
Para el trabajo de refuerzo de décimas, centésimas y milésimas podéis acceder a la página siguiente: http://www.isftic.mepsyd.es/w3/recursos/ primaria/matematicas/decimales/menu.html
Actividad 2
Representación, ordenación y redondeo de números decimales
Para saber qué vale más, una goma de borrar, un lápiz o un compás de madera, deberéis comparar números decimales y saber cuál de ellos es mayor y cuál menor. |
|
Representación
Como sucede con los números naturales, los números decimales también pueden representarse sobre una recta.
Si observáis una regla de las que utilizáis para dibujar y medir, podréis notar que cada unidad se encuentra dividida en diez partes iguales. Cada una de estas partes es una décima. En la recta representada, el punto marcado con la letra E indica el 0,2, A indica el número 3,3 y la letra D indica el número 6,4 ¿Qué números indican las letras F, B y C?
Si aumentamos la imagen y dividimos cada décima en otras diez partes iguales, obtenemos la representación de las centésimas.
De esta forma, ahora, la letra A indicará el número 0,26 y la letra E el número 0,08.
Indicad los números que representan las otras letras.
Si siguiéramos aumentado la imagen, podríamos dividir cada centésima en 10 partes iguales y estaríamos representando las milésimas.
De esta forma, si seguimos aumentando la imagen, podríamos representar cualquier número decimal exacto, por más decimales que tenga.
En el dibujo siguiente podéis comprobar dónde quedaría representado el número 0,137 en la recta numérica:
Como veis en la tabla, al acercarnos lo suficiente al punto rojo, descubrimos que se encuentra sobre el número 0,137:
|
|
Ordenación
La representación sobre una recta de los números decimales nos permite compararlos, es decir, decidir cuál de ellos es el mayor o el menor. Así, cuanto más a la derecha de la recta se encuentre un número decimal mayor será. Sin embargo, no es necesario representarlos para saber cuál de dos números decimales dados es el mayor. Basta con ir comparando sus cifras para determinar cuál de ellos es el mayor.
Ordenar números decimales, es pues, un proceso de comparación.
Comparar dos números decimales puede parecer complicado, si solo nos fijamos en la cantidad de cifras que forman cada uno de los números. Por ejemplo, si tomamos los números 0,42 y 0,402, ¿sabríais indicar cuál de los dos es mayor?
0,402 tiene más cifras que 0,42, sin embargo la respuesta correcta es que 0,42 es mayor que 0,402.
Para comparar números decimales, debemos hacerlo comparando sus cifras por la posición que ocupan. Abrid la siguiente actividad (act2_ordenacion) y ordenad los números decimales que aparecen seleccionando la cantidad que corresponde en cada caso. Recuerda que es una secuencia ordenada, por tanto, al seleccionar un número deberéis tener en cuenta tanto el número anterior como el posterior.
Redondeo
En la vida cotidiana no es práctico utilizar números con muchas cifras decimales, con lo que se suele reducir el número de éstas. Es bastante habitual reducirlas hasta que sólo nos queden 2 decimales, como en el caso de los euros.
Para ello se utiliza el redondeo: se van eliminando las cifras decimales, empezando por la última, la que está situada más a la derecha. ¡ Pero cuidado! Cada vez que se elimina una cifra, si es mayor o igual que 5, se tiene que incrementar en una unidad la cifra anterior, la que se encuentra a su izquierda. En cambio, si es menor que 5, bastará con borrar esa cifra. Este proceso se repetirá para cada cifra que se quiera eliminar, hasta que solo queden dos o tres, para que sea más cómodo manejar el número que ha resultado.
Veamos el siguiente ejemplo:
12,644718 |
Si eliminamos la última cifra, al ser 8 mayor que 5 quedará... |
12,64472 |
Ahora eliminamos el 2, como es menor que 5, quedará... |
12,6447 |
| Ahora os toca continuar a vosotros/as, y deberéis seguir hasta quedaros sólo con dos decimales. |
Haced clic aquí cuando creáis que tenéis la solución.
Dos ejercicios más, dados los números decimales 324,3454 y 6,3465, haz en tu cuaderno el proceso de redondeo hasta llegar a un decimal.
Habéis aprendido a representar, ordenar y redondear los números decimales. Vamos a realizar unos sencillos ejercicios para fijar lo que hemos visto.
Haced clic en la imagen para utilizar la calculadora:
Y si tenéis dudas consultad este manual.
El orden de los decimales:
http://www.skoool.es/content/los/ maths/ordering_dec/launch.html
En este enlace podréis ver la comparación de los números decimales para saber ordenarlos correctamente.
Actividad 2. Segunda parte.
ACTIVIDADES
http://www.i-matematicas.com/Descartes/calculomental/decimales1.htm
Ahora dibujad una recta y situad donde corresponda cada uno de los siguientes números decimales: 3,16 ; 3,61 ; 2,05 ; 2,50
a) 6,89
b) 7,1
c) 7,01
a) 5,345
b) 6,758
c) 0,989898989898…
d) 1,276
e) 12,364
Haced clic en la imagen para utilizar la calculadora:
Y si tenéis dudas consultad este manual.
Actividad 3
Operando con números decimales
Al hacer clic en la imagen de la derecha, observáis una factura y un círculo rojo donde descubriréis sumas y restas con números decimales. Mientras que el círculo azul resalta multiplicaciones de números con decimales. En esta actividad vamos a aprender cómo realizar estas operaciones. |
|
Suma de números decimales
Para sumar números decimales debéis colocarlos alineados verticalmente por la coma, haciendo coincidir las unidades en la misma columna, la coma en la siguiente, las décimas en la columna de su derecha y así sucesivamente, y sumarlos manteniendo la coma en el mismo lugar.
Vamos a ver un ejemplo, en el que sumaremos:
|
|
Resta de números decimales
Para restar números decimales debéis colocarlos alineados por la coma, de la misma forma que hemos observado en la suma, y restarlos manteniendo la coma en el mismo lugar.
¡Pero cuidado!
Antes de iniciar la resta, deberéis rellenar los espacios a la derecha de la coma con los ceros que sean necesarios para que el minuendo tenga el mismo número de cifras decimales que el sustraendo.
Nuevamente, un ejemplo nos ayudará a aclararlo. Restaremos:
|
|
ACTIVIDADES
a) 2,34 + 5, 68
b) 3,24 + 12,01
c) 5,78 + 3, 24
d) 34,3 + 4, 056
a) 5, 68 – 2,34
b) 12,01 – 3,24
c) 5,78 - 3, 24
d) 34,3 - 4, 056
ACTIVIDAD Opcional
Resolved las multiplicaciones siguientes:
a) 5,68 x 2,34
b) 12,01 x 3,24
c) 5,78 x 3, 24
d) 34,3 x 4, 056
- Redondead el resultado de las multiplicaciones a las centésimas.
Si queréis conocer la explicación de cómo multiplicar con números decimales haced clic aquí: Multiplicación de números decimales
Haced clic en la imagen para utilizar la calculadora:
Y si tenéis dudas consultad este manual.
Suma de números decimales:
http://www.skoool.es/content/ los/maths/summ_decimals/launch.html
Suma y resta decimal:
http://www.skoool.es/content/ maths/decimal_add_sub/index.html
Ayuda
- Menú izquierdo (en orden de arriba a abajo): icono página principal de la secuencia (home), icono tamaño de la fuente, icono impresión, icono acceso a la ayuda e icono índice del contenido.
- Barra nombre del material y título de la sección actual.
- Flechas de navegación (página siguiente o anterior).
- Espacio para el contenido.
Autor:
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
Copyright:
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
Recursos
Estos son los recursos TIC que utilizarás para trabajar a lo largo de esta secuencia didáctica:
Procesador de textos Writer (Open Office) |
|
Referencias web recomendables |
|
Un poco de historia
Historia de la coma decimal
1492 |
El matemático italiano Francesco Pellos publica el “Compendio de lo ábaco”, primer documento escrito que se conoce en el que aparece un símbolo como separador entre las cifras de la parte entera y las de la parte decimal. |
||||
1579 |
François Viète (1540-1603), en en su obra “Canon” escribe:
314159|26535 |
||||
1585 |
El matemático flamenco Simon Stevin, acometió la tarea de explicar el uso del separador decimal con todo detalle y de una manera muy elemental y, es el verdadero propagador de la utilización de fracciones decimales. Introduce una notación muy singular. Donde nosotros escribiríamos: 123,4567
123(0) 4(1) 5(2) 6(3) 7(4)
|
||||
1595 |
El suizo Jost Bürgi simplificó la notación eliminando la mención inútil del orden de las fracciones decimales consecutivas y poniendo encima de la cifra de las unidades el signo º. El mismo año, el italiano Magini sustituyó ese redondelito por un punto que colocó entre la cifra de las unidades y la de las décimas. Así nació la notación que todavía se utiliza en nuestros días en los países anglosajones: 123.45 |
||||
Principios del siglo XVII |
El matemático y óptico holandés Wilbord Snellius (1580-1667), conocido también como Willebrord Snell y Willebrord Snel van Royen, introduce el uso de la coma decimal: 123,45 |
||||
Siglo XVIII |
El uso de la coma decimal se extendió por la Europa continental, mientras que en las Islas Británicas el punto decimal se volvió el estándar, tal vez por la influencia de la obra de John Napier. éste, aunque en su “Rhabdologia” usa tanto la coma como el punto, en su importantísima tabla de logaritmos utilizó particularmente el punto decimal. |
||||
Números decimales en la vida cotidiana
Haz clic en la imagen para avanzar:
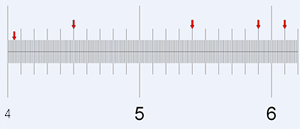
Representación
El punto B indica el número 3,8, el C el número 4,7 y el punto F el número 0,7:
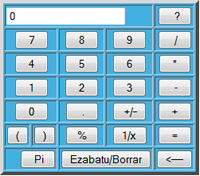
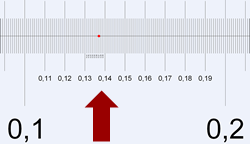
Representación
El punto B indica el número 0,13.
El punto C indica el número 0,43 y el D el número 0,37.
Resultado
Si habéis obtenido la cantidad 12,65 ¡FELICIDADES! Si no os coincide el resultado, revisad los pasos que habéis seguido.
Multiplicación de números decimales
Para multiplicar un número decimal por un número natural, se multiplican los dos números sin tener en cuenta la coma y ésta se coloca de forma que el resultado tenga el mismo número de cifras decimales que el factor decimal.
Veamos cómo se multiplicaría:
|
|
Podréis comprobar que el resultado tiene dos cifras decimales, igual que el multiplicando.
Para multiplicar un número decimal por otro número decimal, se multiplican los dos números sin tener en cuenta las comas y ésta se coloca de forma que el resultado tenga tantas cifras decimales como tienen los dos factores decimales juntos.
Lo veremos mejor con un ejemplo:
|
|
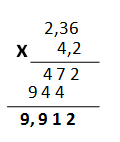
Veréis que el resultado tiene 3 cifras decimales, es decir, tantas como 2 del multiplicando y una del multiplicador.
Para multiplicar un número decimal por 10, 100 ó 1000…, es decir, por un múltiplo de 10, veréis que es muy sencillo. Bastará con desplazar la coma hacia la derecha desde su posición inicial, tantos lugares como ceros acompañan a la unidad. Si se acaban las cifras, solo deberéis añadir los ceros que sean necesarios a la derecha del último número.
La secuencia que os presentamos a continuación os ayudará a verlo más claro :
Observamos que, mientras en los dos primeros casos, hemos podido desplazar la coma sin problemas, en el tercer caso hemos añadido un 0 a la derecha del 5, para poder desplazar la coma las 3 posiciones que nos indica el número 1000, ya que tiene 3 ceros.